[¯|¯] Relazioni in un insieme. Proprietà riflessiva, proprietà simmetrica, transitiva, antisimmetrica
giovedì, Giugno 21st, 2018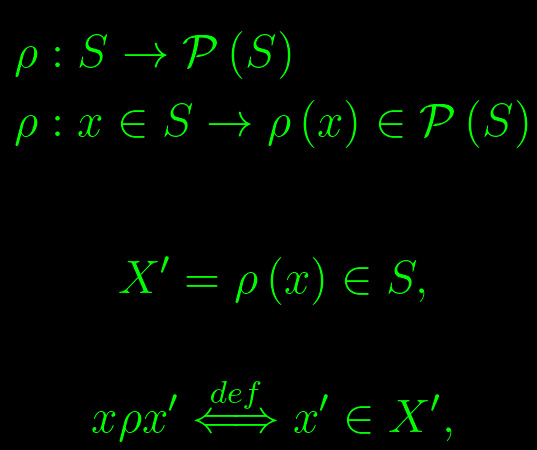
In una lezione precedente abbiamo introdotto la nozione di corrispondenza tra insiemi. Oggi parleremo di relazione tra gli elementi di un assegnato insieme.
Definizione
Comunque prendiamo un insieme non vuoto S, dicesi relazione una qualunque corrispondenza di S su sé stesso, i.e. una corrispondenza da S verso S:

Posto

scriviamo

che si legge "x è in relazione con x'".
Per quanto precede, l'assegnare una relazione ρ in S, determina univocamente la corrispondenza inversa

ove
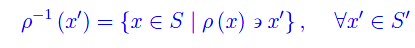
Definizione
Chiamiamo ρ-1 relazione inversa
Proposizione
Comunque prendiamo x,x' quali elementi di S, x è in relazione con x' se e solo se x' è in relazione inversa con x.
Dimostrazione
Esaminiamo ora alcune proprietà che possono essere verificate da una relazione assegnata.
- Proprietà riflessiva
Una relazione ρ:S->P(S) verifica la proprietà riflessiva se
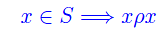
- Proprietà simmetrica
Una relazione ρ:S->P(S) verifica la proprietà simmetrica se
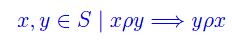
- Proprietà antisimmetrica
Una relazione ρ:S->P(S) verifica la proprietà antisimmetrica se
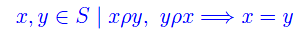
- Proprietà transitiva
Una relazione ρ:S->P(S) verifica la proprietà transitiva se
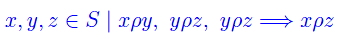

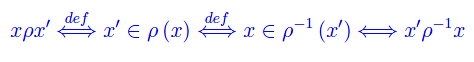



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











