Le figure di Norton Starr

venerdì, Giugno 25th, 2021

norton starr, figure,mathematica — **Fig. 1**

Sia γ un luogo geometrico del piano di rappresentazione parametrica regolare

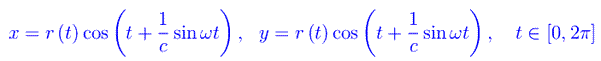
dove

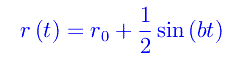
Qui è r₀ > 0, mentre b,c,ω sono interi naturali. Si noti che per ω=b=0,c=1, il luogo è la circonferenza di centro l'origine e di raggio r₀. Per b=8,c=4,ω=16 si ottiene la curva di fig.

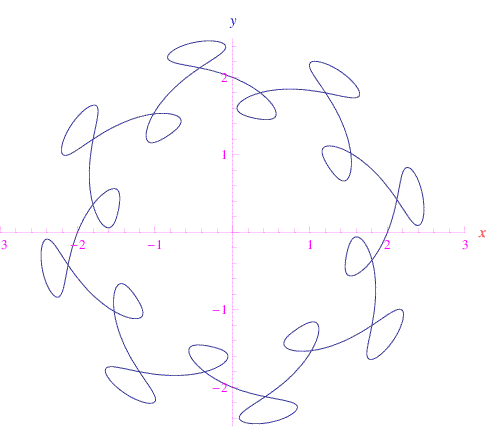
L'idea di Norton Starr consiste nell'utilizzare l'ambiente di calcolo Mathematica per tracciare il vettore posizione di un punto mobile sul luogo (eqluogo) per poi sottopporre a una successione di espansioni/contrazioni i perimetri delle figure ottenute, generando immagini di singolare bellezza, come riportato in fig. 1.

Per generarli con Mathematica abbiamo riadatto il codice originale di Norton Starr (che girava su una delle prime versioni di Mathematica):

(altro…)

Posted in Digital Art, Mathematica | No Comments »

Una inusuale variante di un moto circolare

domenica, Febbraio 21st, 2016

Una interessante variante di un programma elaborato da Norton Starr e proposta da Stan Vagon produce l'immagine animata al top di quest'articolo.
(altro…)