[¯|¯] Funzione dissipativa e potenza dissipata istantanea
sabato, Marzo 4th, 2017
Nel post precedente abbiamo introdotto la nozione di valore efficace di una funzione continua. Procediamo ora con la seguente definizione:
Definizione 1
Comunque prendiamo un elemento f dello spazio funzionale C([a,b]), chiamiamo funzione dissipativa associata a f l'elemento di C([a,b]) dato da

essendo ß un numero reale positivo assegnato.
Definizione 2
La potenza istantanea dissipata dalla Rf(x) è

Da ciò segue che il valor medio di Wf(x) è:
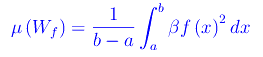
Cioè

Per esplicitare il significato di tali locuzioni consideriamo il seguente esempio tratto dalla meccanica classica: una particella di massa m si muove lungo l'asse x in un campo di forze F(x) e sotto l'azione di una forza viscosa, come illustrato in figura:

Diagramma delle forze agenti sulla particella. F è la forza attiva, mentre R è la resistenza passiva (forza viscosa).
In regime lineare
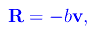
dove b>0 e v è il vettore velocità. Per la seconda legge di Newton:
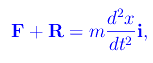
essendo i il versore dell'asse x. Proiettando tale equazione vettoriale sull'asse x, otteniamo l'equazione scalare:

Cioè

avendo definito il coefficiente di smorzamento per unità di massa:
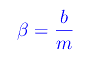
Abbiamo così ottenuto un'equazione differenziale lineare del primo ordine in v(t). Per F=0 tale equazione è omogenea, per cui abbiamo il seguente problema di Cauchy:

la cui unica soluzione è
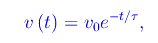
dove

è una costante di tempo. Precisamente:

L'energia meccanica della particella si riduce al solo termine cinetico, giacché stiamo considerando F(x)=0. Quindi

Tale risultato è consistente, perché l'energia cinetica iniziale

viene dissipata dalla forza viscosa tramite un fattore di smorzamento esponenziale. L'energia dissipata per unità di tempo i.e. la potenza dissipata è

Se ci riferiamo all'unità di massa:

il cui valor medio nel tempo è:

dove
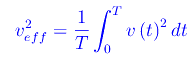
(altro…)



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











