[¯|¯] La costante di Feigenbaum, la costante di struttura fine e l'età dell'Universo
venerdì, Dicembre 25th, 2015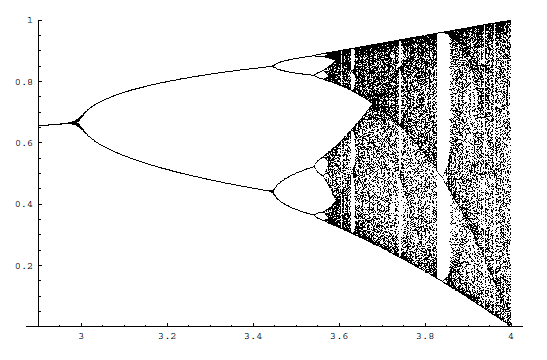
Sto leggendo Se questo è l'infinito del fisico Emilio Santoro.
Sono ancora all'"inizio", considerando la lunghezza del libro (oltre 700 pagine). Ieri sera, navigando nell'indice ho trovato un capitolo interessante (al di là dell'impianto narrativo, di per sé eccellente). Il protagonista, "quasi" l'alter ego dell'autore (per esigenze narrative), è un astrofisico che si imbatte in uno strano legame tra la costante di Feigenbaum, la costante di struttura fine, pi greco e l'età dell'universo. Tale legame è solo l'inizio di una teoria elaborata dall'autore e che si sviluppa nelle pagine successive, e che tuttavia ha suscitato il mio interesse, poichè in un vecchio articolo avevo trattato la mappa logistica in ambiente Mathematica. L'articolo può essere letto a questo link (pagg. 61 e s.), la cui idea di partenza è che la mappa logistica altro non è che un'equazione differenziale del tipo Bernoulli-Riccati che regola l'evoluzione di un sistema dinamico a tempo continuo, scritta "nel tempo discreto" (per essere più precisi, si tratta di un automa cellulare). Incidentalmente, un sistema a tempo continuo governato da un'equazione del tipo Bernoulli-Riccati non è caotico (pur essendo non lineare). Ne consegue che il caos deterministico non è di origine fisica, ma computazionale. In tal modo l'esistenza in natura del caos deterministico non farebbe altro che corroborare l'interpretazione pitagorica dell'universo (in forza dell'origine computazionale, quindi numerica del caos).


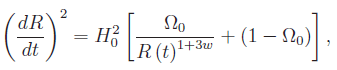


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











