[¯|¯] Caos deterministico o computazionale?

Febbraio 1st, 2015 | by Marcello Colozzo |

Ho lasciato per ultima l'introduzione dell'articolo (in realtà l'articolo è tutt'altro che completo). La intro prenderà le mosse dall'utilizzo del sistema di navigazione inerziale a bordo dei razzi V2 durante la seconda guerra mondiale. Da un archivio storico è, però, emerso che il primo - rudimentale - sistema di navigazione inerziale venne utilizzato a bordo dell'U-boat 107 durante l'Operazione Paukenschlag.

Nella mia simulazione di questo sistema di navigazione inerziale ho volutamente modificato il numero dell'U-boat in 130 e facendolo partire dalla base di La Rochelle (ricordo che si tratta di una simulazione per mostrare l'origine computazionale del caos deterministico della mappa logistica).

L'accelerometro dell'U-boat darà in pasto al calcolatore di bordo (esistevano a quei tempi? Credo di no 🙂 ) la derivata prima della velocità, per cui nell'ipotesi di un moto unidimensionale, viene generato il seguente Problema di Cauchy:

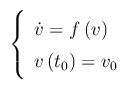
Notiamo che anche qui sono state fatte delle ipotesi semplificatrici, e cioè la scelta di una f(v), anzichè una f(t,v,dv/dt). Ma ciò è voluto, poichè vogliamo riferirci alla classe dei sistemi autonomi.
Lo step successivo consiste nello scegliere una f(v) in grado di generare (dopo aver applicato il Metodo di Eulero) la mappa logistica. E allora, proviamo ad immaginare uno scenario in cui il calcolatore di bordo conosce come unico algoritmo proprio il Metodo di Eulero. Conseguentemente, entrerà in un loop caotico mettendo in evidenza non tanto i limiti del sistema di navigazione inerziale, bensì la vera origine (non fisica) del caos deterministico e cioè l'approssimazione indotta dall'algoritmo di Eulero. Sarebbe allora il caso di rodefinirlo come caos computazionale.