[¯|¯] Il libero arbitrio: una questione termodinamica?

Novembre 29th, 2014 | by Marcello Colozzo |

Dalla condivisione dello stato di Facebook di uno dei miei contatti:

mi sono venute alcune idee sulla questione del cosiddetto libero arbitrio. Una precisazione: le suddette idee vanno prese con le molle, perchè si tratta di speculazioni (deliri? 🙂 ) e nulla di più.
Ciò premesso, denotiamo con X un qualunque sistema cognitivo (umano, calcolatore). In poche parole, X è un sistema "in grado di pensare" e, soprattutto di ricordare (in effetti, il nocciolo della questione è legato alla memoria). Osserviamo subito che se X è un calcolatore, la sua memoria è praticamente infallibile. Ciò è dovuto al valore estremamente basso dell'entropia dei suoi stati logici. Infatti, la memoria di un calcolatore è un sistema a due stati, e utilizzando la nota formula (dalla meccanica statistica), si ottiene per l'entropia (k_B è la costante di Boltzmann):

entropia,termodinamica,meccanica statistica

Se, invece, X non è un calcolatore:

dove 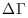è il volume dello spazio delle fasi associato al sistema, i.e. il numero di stati di singola particella. È chiaro che qui 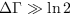, onde una qualunque interfaccia umana avrà un'entropia del proprio sistema cognitivo, maggiore dell'entropia della memoria di un calcolatore. In altre parole, un calcolatore ha una "memoria infallibile" proprio perchè è un sistema "più ordinato".

Ma ciò non inficia il ragionamento che segue. Fondamentalmente, ricordare equivale a creare un maggiore ordine nell'insieme degli stati o, ciò che è lo stesso, diminuire l'entropia. Siccome i pensieri si realizzano grazie a processi di natura elettrochimica e questi ultimi sono inevitabilmente dissipativi, segue che il calore generato viene ceduto all'ambiente esterno. E, in ultima istanza, all'universo che qui denotiamo con U. Ciò è in accordo con il secondo principio della termodinamica: U è un sistema isolato e la sua entropia non può fare altro che aumentare. In altre parole, ad una diminuzione dell'entropia di X segue necessariamente un aumento dell'entropia di U. E anche questa conclusione è in accordo con il suddetto principio, giacchè X non è un sistema isolato, per cui la sua entropia può diminuire.

Come è noto, l'entropia crescente di U individua la cosiddetta freccia del tempo termodinamica che rompe la simmetria rispetto al tempo, orientando il passato verso il futuro. Siccome l'atto di pensare per ogni sistema cognitivo X (umano, calcolatore) aumenta l'entropia di U, concludiamo che ogni X pensa nel verso dell'entropia crescente di U.
Ipotizziamo, ora, l'esistenza di un sistema cognitivo onnisciente O. Per definizione di onniscienza, O conosce tutto, inclusa la sua evoluzione futura. In poche parole, sa cosa accadrà nel futuro. Se così non fosse, esisterebbe almeno un elemento che O non conosce, onde non sarebbe onnisciente. La prima conseguenza è che tutto ciò che riguarda l'attività cognitiva/memoria di O non avviene tramite processi elettrochimici (neuroni) o elettronici (circuiti integrati di un calcolatore). Tale sistema non ricorda solo il passato, ma anche il futuro. La seconda conseguenza riguarda il libero arbitrio: un qualunque sistema cognitivo X è dotato di libero arbitrio, i.e. compie delle scelte, in quanto non conosce il futuro. Di contro, un qualunque sistema onnisciente è privo di libero arbitrio, poichè conosce il futuro (quindi non compie alcuna scelta perchè sa già cosa accadrà). In un certo modo, la spinosa questione del libero arbitrio, sembrerebbe essere collegata al secondo principio della termodinamica.

No TweetBacks yet. (Be the first to Tweet this post)