Esercizio di elettrostatica risolto con la legge di Gauss
Dicembre 19th, 2022 | by Marcello Colozzo |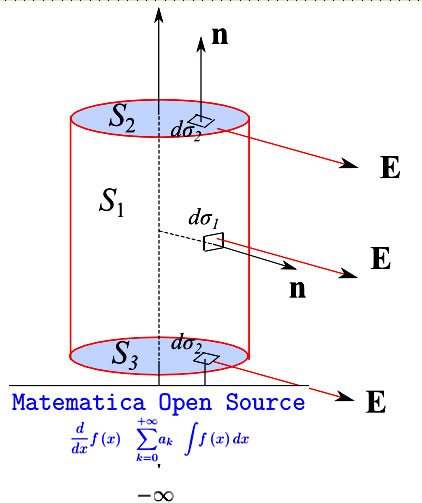
Esercizio
Risolvere l'esercizio applicando la legge di Gauss
Soluzione
In unità SI e con ovvio significato dei simboli:
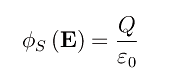
La simmetria cilindrica del problema suggerisce di assumere come superficie S, quella del cilindro circolare retto di asse z e altezza L come illustrato in fig.
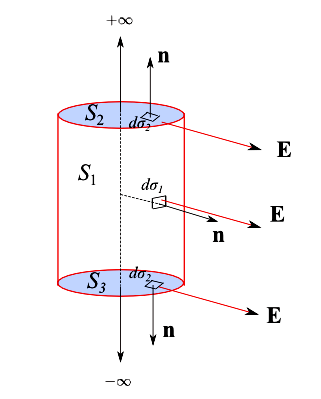
da cui vediamo che:
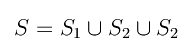
Procedendo per decomposizione nell'integrale di superficie che esprime il flusso del campo elettrico:
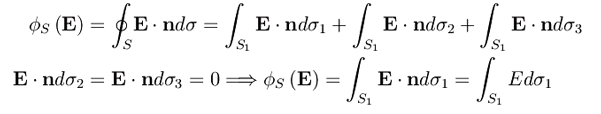
In virtù della simmetria cilindrica è E=E(r) cioè il campo dipende dalla sola coordinata radiale (siamo in coordinate cilindriche) r che è poi il raggio del cilindro della fig. precedente. L'elemento di superficie di S
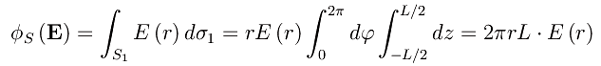
Per la legge di Gauss:
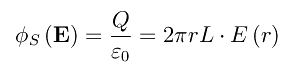
Siccome si suppone nota la densità di carica lineare (ρ0=costante) lungo l'asse del cilindro, si ha che Q=ρ0L, onde dalla precedente equazione
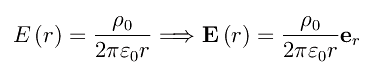




 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











