Calcolo dimensionale delle aste di una gru

Novembre 8th, 2021 | by Marcello Colozzo |

scienza delle costruzioni,gru,calcolo dimensionale — **Fig. 1**

Esercizi di Scienza delle Costruzioni elaborati dell'ing. Giorgio Bertucelli.

Esercizio

Calcolo dimensionale delle aste della gru di fig. 1.

Soluzione

In una struttura reticolare, dove tutti i nodi sono cerniere, le forze interne alla struttura si riducono a soli sforzi normali alle sezioni delle aste; gli sforzi agiscono sulle aste o a trazione -- tiranti -- o a carico di punta -- puntoni (in rosso). La procedura di calcolo è la seguente.

Dati i carichi di progetto, si calcolano le reazioni vincolare esterne. Nel nostro caso la gru è una struttura isostatica. Dato il carico esterno P le reazioni vincolari in A (cerniera con carrello) e in B (cerniera) sono:
Si sceglie una scala per disegnare i vettori dei carichi e delle reazioni vincolari.
Si inizia dal primo nodo esterno di fig. 2, a sinistra, in cui confluiscono tre sforzi; ciò affinché sia possibile la scomposizione delle forze. Allo stesso modo si procede per tutti gli altri nodi in cui sono applicate le reazioni vincolari.

Fig. 2
Si può quindi procedere con gli altri nodi, nei quali la somma vettoriale degli sforzi dovrà annullarsi. Scelto un nodo, si procederà, rispettando un senso di rotazione e partendo dallo stesso nodo, alla somma vettoriale degli sforzi il cui risultato porterà a disegnare un poligono chiuso: punto di partenza e d'arrivo devono coincidere. In forza della scala di disegno scelta è ora possibile misurare, con lo scalimetro, il valore di uno sforzo su un'asta della struttura reticolare (fig. 3).

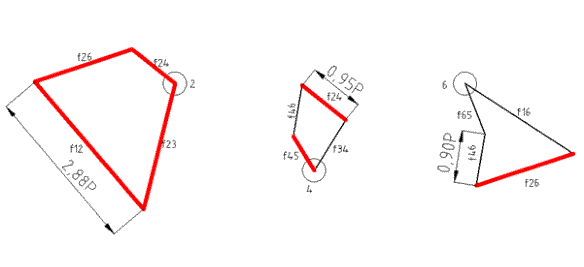
Fig. 3

Tiranti

Dalla Scienza delle Costruzioni sappiamo che l'allungamento del tirante (fig. 4) è dato da:

dove A è l'area della sezione del tirante (mm²), mentre E è il modulo di elasticità di Young (N /mm²).

La dilatazione:

dove σ_amm è la sollecitazione massima ammissibile del materiale impiegato (N /mm²). Pertanto si può scrivere

Puntoni
Dalla Scienza delle Costruzioni, sappiamo che lo sforzo critico (fig. 5) è dato da:

dove J è il momento d'inerzia, mentre l è la lunghezza dell'asta.

L'area A della sezione del puntone viene calcolata nel sistema "ω" in uso nelle norme tedesche fin dal 1925. Scelto k₀ ((N /mm²) carico di sicurezza del materiale, scriveremo:

I valori di ω in funzione del rapporto di snellezza λ del puntone e del tipo di acciaio impiegato sono riportate nelle Norme Costruttive DIN tedesche, UNI italiane e così via.

Indice degli esercizi

No TweetBacks yet. (Be the first to Tweet this post)