[¯|¯] Diodo a semiconduttore sottoposto a un segnale immerso in un white noise
Giugno 22nd, 2018 | by Marcello Colozzo |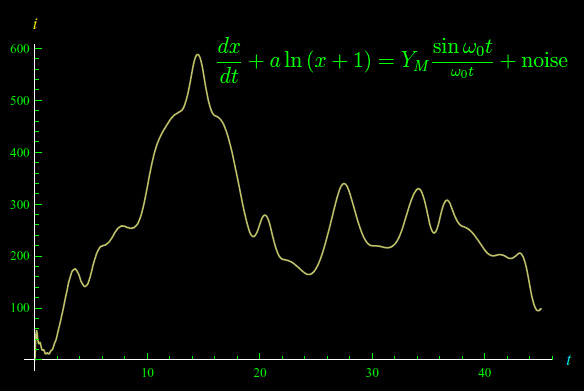
Ricordiamo che l'intensità di corrente i in un diodo è data da
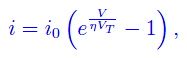
dove i0 è la corrente di saturazione inversa, VT una grandezza con le dimensioni di una differenza di potenziale dipendente dalla temperatura assoluta T, e infine η è un coefficiente adimensionale dipendente dal materiale semiconduttore con cui è costruito il diodo. Adimensionalizzando le varie grandezze si perviene a
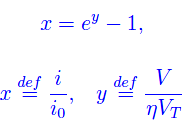
Supponiamo che y sia un'oscillazione sinusoidale modulata da un 1/t, i.e. una funzione sinc:
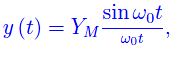
dove YM è l'ampiezza, mentre ω0>0 ha le dimensioni di una pulsazione. L'intensità di corrente è
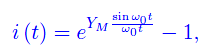
graficata nella fig. seguente, da cui vediamo l'effetto raddrizzatore del diodo:
Per tener conto di un eventuale coefficiente di autoinduzione, è necessario aggiungere in serie al diodo una induttanza, per cui la caduta di tensione ai capi di quest'ultima è
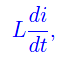
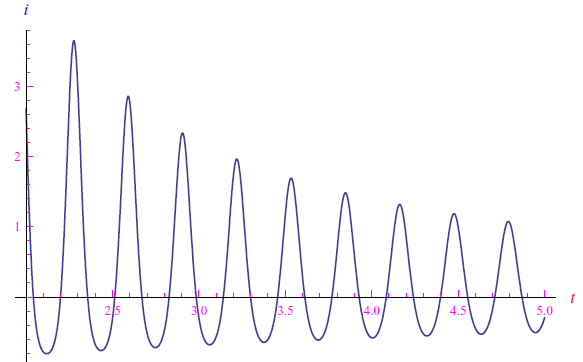
dove L è il coefficiente di autoinduzione. Applicando il secondo enunciato di Kirchoff e adimensionalizzando, si perviene a un'equazione differenziale
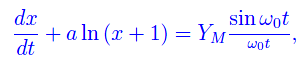
dove a>0 è un parametro che tiene conto delle varie grandezze fisiche sottoposte ad adimensionalizzazione. Tale equazione differenziale va integrata con la condizione iniziale i(0)=0. Per YM=700,a=0.1 e ω0=20rad/s, otteniamo l'andamento graficato in figura:
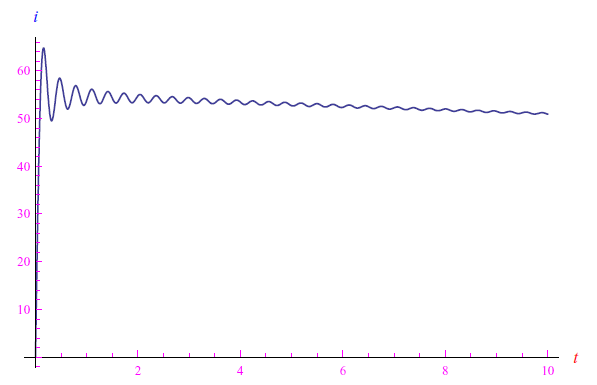
Infine, supponendo che il segnale di ingresso i.e. la d.d.p che alimenta la serie sia immerso in un white noise, l'integrazione numerica della corrispondente equazione differenziale, si perviene al grafico riportato nella figura al top di questa pagina.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
Tags: diodo, funzione sinc, segnale, white noise
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











