[¯|¯] Interpretazione della funzione d'onda. Max Born vs Schrödinger
Maggio 18th, 2017 | by Marcello Colozzo |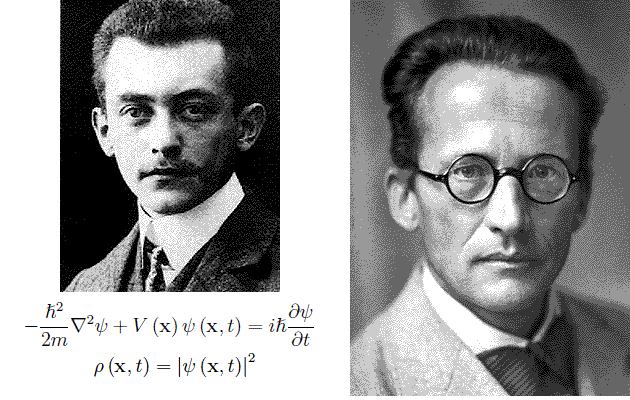
In previous issues we physically interpreted the wave function through the following functional identity:
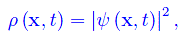
where ρ(x,t) is the probability density for the location, meaning the differential magnitude
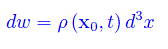
is the infinitesimal probability of finding the particle in the infinitesimal volume d³x centered at time t in x0. Initially Schrödinger interpreted the quantity ψ defining |ψ|2 as the electric charge density at time t at the point x. It should be borne in mind that electrically neutral particles were unknown at the time.
Nei numeri precedenti abbiamo interpretato fisicamente la funzione d'onda attraverso la seguente identità funzionale:
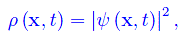
dove ρ(x,t) è la densità di probabilità per la posizione, nel senso che la grandezza differenziale
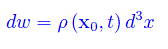
è la probabilità infinitesima di trovare al tempo t la particella nel volume infinitesimo d³x centrato in x0. Inizialmente Schrödinger interpretò in maniera diversa la grandezza ψ definendo |ψ|2 come la densità di carica elettrica al tempo t nel punto x. È da tener presente che all'epoca erano sconosciute le particelle elettricamente neutre.
Tags: funzione d'onda, max born, meccanica quantistica, schrödinger
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











