Capacità di un condensatore piano
Dicembre 24th, 2022 | by Marcello Colozzo |
Legge di Gauss
Riprendiamo la lezione sul condensatore. Consideriamo il caso particolare di n=2 conduttori costituiti da due piastre parallele separate da una distanza d. Ogni piastra è uniformemente carica, una con cariche positive, l'altra con cariche negative. Abbiamo in questo modo realizzato un condensatore piano, e le piastre sono le sue armature. È essenziale osservare che esse sono separate da uno spazio vuoto i.e. siamo in assenza di materia. Per determinare la capacità del condensatore piano, calcoliamo innanzitutto il campo elettrico generato dalle armature. Queste ultime sono modellizzabili attraverso due piani paralleli uniformemente carichi, anche se in tal modo trascuriamo gli effetti di bordo dovuti al fatto che le armature hanno estensione limitata. In base a una proprietà dimostrata in una lezione precedente il campo elettrico E è perpendicolare alle armature. Calcoliamo E utilizzando la legge di Gauss. A tale scopo dobbiamo assegnare l'appropriata superficie gaussiana, e la scelta giusta è quella di un cilindro disposto come in fig. 1.
Quindi
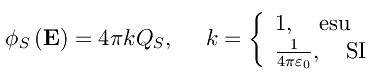
Esplicitiamo il primo membro:
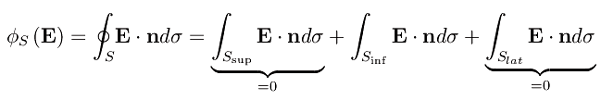
per cui
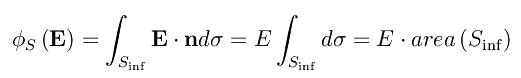
Esplitiamo il secondo membro dell'equazione che esprime la legge di Gauss:
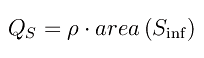
Ora la legge di Gauss assume la forma
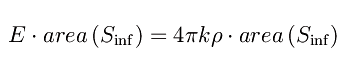
che ci consente di ricavare il campo elettrico:
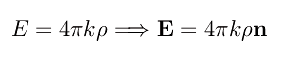
Determiniamo ora il potenziale V. A tale scopo orientiamo una terna cartesiana Oxyz con il piano coordinato xy coincidente con l'armatura 1 (supposta illimitata). Quindi, il versore n altro non è che il versore dell'asse z cambiato di segno, cosicché:
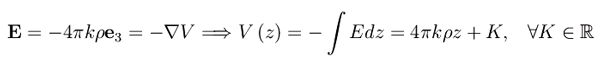
Il potenziale dell'armatura 1 è V1=V(0)=K, mentre il potenziale dell'armatura 2 è V2=V(-d)=-4pkρd. Per definizione di capacità, l'armatura 2 è consderata al potenziale 0, e la capacità del condensatore è
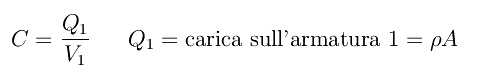
essendo A l'area di singola armatura. Allora
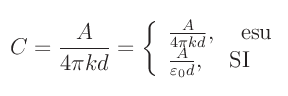



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











