Introduzione al condensatore
Dicembre 22nd, 2022 | by Marcello Colozzo |
L'energia elettrostatica di una distribuzione di carica ρ(x) è
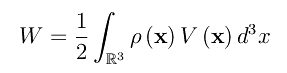
dove V(x) è il potenziale del campo elettrostatico generato dalla predetta distribuzione:

Ciò premesso, consideriamo n conduttori disposti secondo una assegnata geometria. Supponiamo che ogni conduttore sia elettricamente carico e denotiamo con Qi la carica totale del conduttore i-esimo. Dall'equazione precedente vediamo che il potenziale si comporta alla stregua di un operatore lineare. Nel caso particolare degli n conduttori tale linearità implica

dove pij sono coefficienti reali che dipendono dalla geometria dei conduttori. È ragionevole assumere
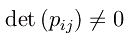
per cui le equazioni scritte sopra compongono un sistema di equazioni lineari nelle n incognite Qi e termini noti Vi. Il non annullarsi del determinante della matrice dei coefficienti, rende tale sistema compatibile e determinato. Risolvendo con la regola di Cramer, l'unica soluzione si scrive come:

I coefficienti Cij si chiamano coefficienti di induzione se i diverso da j, mentre per i=j abbiamo i coefficienti di capacità (o semplicemente capacità) Cii. Per rendere più chiara l'esposizione, scriviamo per esteso le soluzioni:
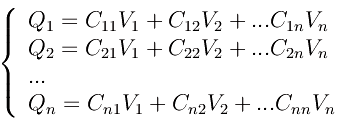
dove vediamo che la capacità dele conduttore 1 è la sua carica totale Q1, quando esso è mantenuto al potenziale unitario:
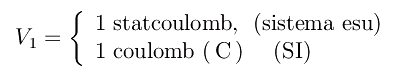
mentre i rimanenti sono mantenuti a potenziale zero. Cioè
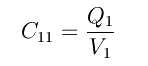
che si generalizza immediatamente
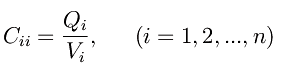



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











