» Esercizi svolti di Matematica e Fisica

Cos'è la divergenza di un campo vettoriale?

Dicembre 18th, 2022 | by Marcello Colozzo |

---

---

Esercizio
Dimostrare la formula riportata in fig. 1.

---

Soluzione

Rammentiamo innanzitutto il teorema della divergenza:

essendo D un dominio regolare di R³, mentre n e dσ sono rispettivamente la normale esterna e l'elemento di superficie della frontiera di D.
Osservazione
Sul "Smirnov" (fig. 1 tale teorema è noto come «formula di Ostrogradskij».)
Come è noto, il secondo membro del teorema della divergenza è il flusso del vettore A uscente dalla frontiera di D:

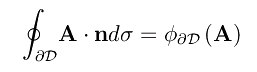
Assumendo assegnato D e quindi una qualche rappresentazione (implicita, parametrica, etc.) della superficie "frontiera di D", è in linea di principio possibile esprimere l'elemento di superficie vettoriale ndσ, dopodiché calcolare l'integrale di superficie ridotto a un ordinario integrale doppio.
Ciò premesso, fissato ad arbitrio un dominio T contenuto in D, per il teorema della media integrale:

per cui

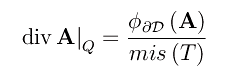
Fissato ad arbitrio P in T e contraendo T su Q, necessariamente Q->P, cosicché

Questa operazione di passaggio al limite suggerisce la seguente definizione:

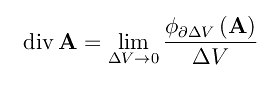
essendo il numeratore a secondo membro il flusso di A attraverso una «piccola superficie» (i.e. al limite infinitesima) che racchiude il punto P in cui calcoliamo divA.

Articoli correlati