Circuito raddrizzatore a ssemplice semionda (esperienza di laboratorio di elettronica)

Novembre 26th, 2022 | by Marcello Colozzo |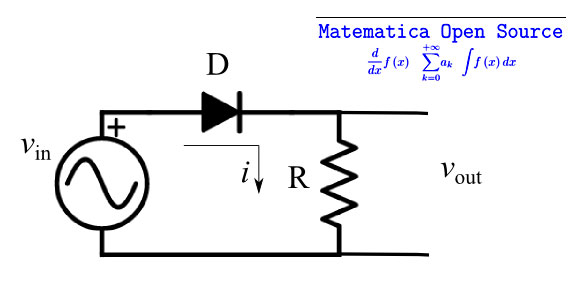

raddrizzatore a semplice semionda,diodo,laboratorio di elettronica — **Fig. 1.**

Da un punto di vista circuitale il caso del diodo a giunzione è atipico, non solo in virtù del comportamento non lineare, ma anche perchè a differenza dei componenti passivi L,C, l'applicazione dei principi di Kirchhoff non restituisce un'equazione differenziale (o integro-differenziale). Consideriamo quindi un raddrizzatore a semplice semionda secondo lo schema di fig. 1. Se v è la tensione ai capi del diodo, per il secondo principio di Kirchhoff si ha:

La corrente è data da:

dove η è un parametro adimensionale (pari a 1 per il germanio e circa 2 per il silicio), mentre V_T è l'equivalente in volt della temperatura. Considerando un diodo al germanio, si ha

Dalle equazioni scritte sopra si ricava facilmente

dove abbiamo considerato un ingresso sinusoidale. Per R=10kO ,V_{M}=120V ,?=500prad/s , risolvendo con Mathematica otteniamo gli andamenti graficati nelle seguenti figure:

Infine, simulando un white noise con Mathematica possiamo verificare l'effetto raddrizzatore in presenza di un segnale di ingresso sinusoidale rumoroso.