«Gas» di francobolli
Febbraio 25th, 2022 | by Marcello Colozzo |
Il sistema fisico in esame è composto da N particelle (=francobolli) non interagenti e «appoggiate» sulla scrivania. Ne segue che le forze agenti sulla singola particella, sono: P=mg (peso) e la reazione normale del vincolo R=-P, per cui la particella è è in quiete. Tuttavia, abbiamo una energia termica:
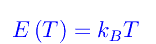
dove kB è la costante di Boltzmann e T la temperatura di equilibrio termodinamico. Siccome stiamo considerando «oggetti classici» (più precisamente, un gas ideale di particelle), la funzione di distribuzione (i.e. densità di probabilità) di trovare una particella nell'elemento di volume dV=dxdydz, è

dove H(x,y,z,p_{x},p_{y},p_{z}) è l'hamiltoniana di singola particella, mentre A è una costante di normalizzazione, cioè tale che
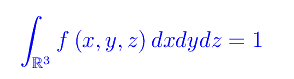
da cui
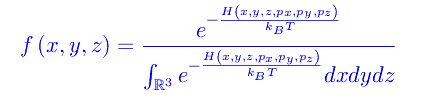
nota come distribuzione di Boltzmann. Nel nostro caso l'hamiltoniana di singola particella è H(x,y,z)=V(x,y,z) essendo questa l'energia potenziale del campo di forze gravitazionali. Precisamente, orientando la terna di assi cartesiani Oxyz con il piano coordinato xy coincidente con il piano della scrivania, e l'asse z orientato verso l'alto, si ha V(z)=mgz. Quindi la probabilità di trovare un francobollo alla quota z è

Sostituendo i dati numerici, otteniamo:
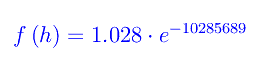



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











