Cilindro con gas immerso in un bagno termico

Gennaio 16th, 2022 | by Marcello Colozzo |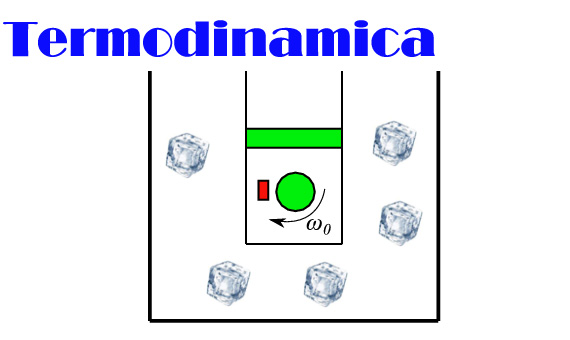

Esercizio

Un cilindro è immerso in un bagno termico costituito da una massa d'acqua M e da cubetti di ghiaccio (per una massa complessiva m). A sua volta il cilindro è riempito da una mole di gas perfetto chiuso da un pistone in equilibrio grazie alle forze di pressione (costante) esercitata dal gas (fig. 1).

Nel volume occupato dal gas, un volano è in rotazione uniforme (I=momento di inerzia, ω₀=velocità angolare). L'intero sistema è in equilibrio alla temperatura T₀=273.15K. Ad un certo istante viene azionato un freno che rallenta il volano fino alla quiete. Se C è la capacità termica del volano (si trascuri quella del freno), determinare al temperatura finale del sistema e il lavoro compiuto dal gas.

Soluzione

Fino a quando non viene azionato il freno, l'energia cinetica del volano è

Per fondere il ghiaccio è necessaria una quantità di calore

dove λ=80cal/g è il calore latente di fusione del ghiaccio. In seguito all'azione del freno, l'energia cinetica E₀ viene progressivamente dissipata in calore. Abbiamo, dunque

per cui il sistema permane nello stato di equilibrio alla temperatura T₀.

Dal momento che non è disponibile altra energia, il sistema permane nello stato di equilibrio alla temperatura T₀. Il caso più interessante è E₀0 > Q_L. Al termine della fusione del ghiaccio, il volano ha un'energia

che verrà dissipata in una quantità di calore di cui una parte verrà assorbita dal volano:

dove ΔT è l'incremento di temperatura del volano. Per le ipotesi fatte, tale incremento è comune all'intero sistema bagno+gas+volano. Il calore rimananente verrà assorbito dal bagno termico di massa (d'acqua) m+M:

essendo c=1 cal/K è il calore specifico dell'acqua. Quindi il calore ceduto è in valore assoluto

Ricordiamo che una quantità di calore è positiva quando è assorbita dal sistema, e viceversa. Nel nostro caso il calore è ceduto, per cui

A sua volta il gas si espande isobaricamente (P=costante) compiendo un lavoro

L'incremento di volume può essere valutato approssimativamente, utilizzando l'equazione di stato PV=RT.
Per il primo principio della termodinamica:

per cui dobbiamo determinare la variazione di energia interna del gas. Includendo l'energia cinetica del volano:

dove

Si noti che l'energia iniziale non E₀ ma E'₀ cioè quella nell'istante di fusione completa del ghiaccio. Tenendo conto di tutte le relazioni trovate, si ha