Calcolo del coefficiente di viscosità di un fluido
Dicembre 15th, 2021 | by Marcello Colozzo |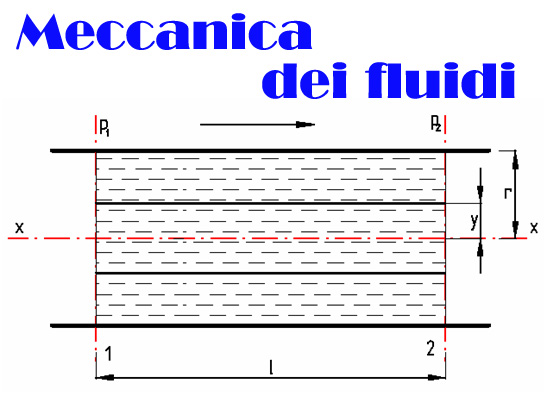
Esercizio
In un condotto cilindrico di raggio r (fig. 1) scorre un fluido viscoso di moto laminare e stazionario, la cui portata è V(m³/s); si conoscono le pressioni statiche p
Soluzione
Ammettiamo che in ogni punto la velocità del fluido è parallela all'asse del condotto. Per simmetria in tutti i punti di una medesima sezione, equidistanti dall'asse del condotto, la velocità u ha il medesimo valore; u è quindi funzione della distanza y tra il punto considerato e l'asse del condotto.
Osservando la fig. 1 scriveremo:

Dunque l'equazione di continuità
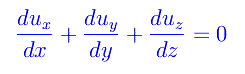
diventa:
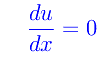
Ne consegue che la distribuzione della velocità è identica in tutte le sezioni e quindi u è funzione della sola l. Le forze in gioco sono:
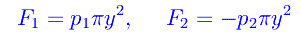
La forza tangenziale parallela all'asse x e dovuta a u(y) è

Scriveremo quindi

Quindi
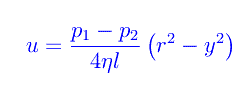
Osserviamo che
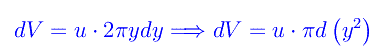
Cioè
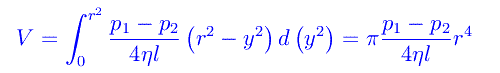
da cui ricaviamo la viscosità:
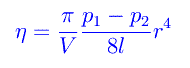



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











