» Esercizi svolti di Matematica e Fisica

Classificazione dei punti singolari di un'equazione differenziale

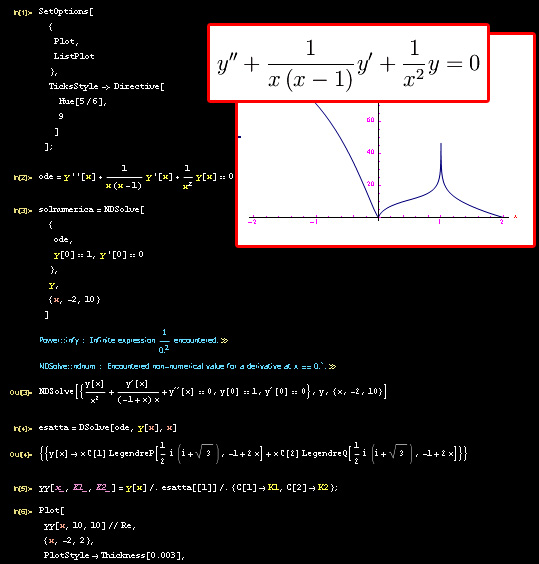
Esercizio

Classificare gli eventuali punti singolari dell'equazione differenziale rappresentata in fig. 1.

Soluzione
Scriviamo l'equazione nella forma:

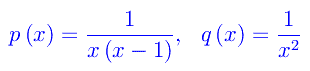
Ne segue che x₀=0,x1=1 sono punti singolari. Per classificarli, determiniamo

entrambe analitiche. Quindi x₀=0 è punto singolare regolare. Passiamo al secondo punto; qui dobbiamo testare solo p(x)

che è ivi analitica. Ne concludiamo che i punti singolari trovati sono regolari. In fig. fig:sing il grafico di uno degli integrali dell'equazione differenziale proposta, ottenuto con Mathematica, da cui vediamo che i punti x=0 e x=1 sono di discontinuità per la derivata prima (rispettivamente un punto angoloso e un punto cuspidale).