Introduzione alla tassellatura di Penrose

Luglio 28th, 2021 | by Marcello Colozzo |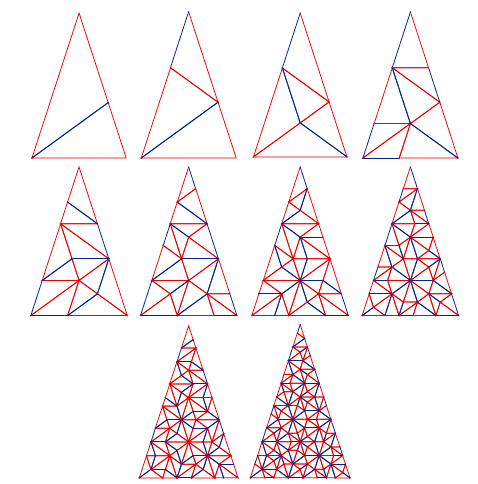

Rammentiamo che la sezione aurea è

Questo numero irrazionale è una delle radici dell'equazione x²-x-1=0, onde

Ciò premesso, i pattern della tessellatura di Penrose sono i triangoli isosceli T₍₊₁₎ e T_(-1):

come illustrato in fig.

Dalla stessa figura vediamo che i predetti triangoli possono essere accoppiati omonimamente in modo da restituire rispettivamente un aquilone e una freccia.

Il processo di tassellatura è inizializzato dal triangolo T₍₊₁₎, eseguendo una dissezione che genera un triangolo T_(-1) annidato nel precedente. L'iterazione del processo per un numero finito di passi, restituisce la fig. 1. Concentriamoci sul secondo triangolo di tale figura. Se lo dilatiamo di un fattore f possiamo piazzare 3 tasselli. Passiamo al quarto triangolo: dilatiamolo di un fattore φ², ruotiamolo in modo da sovrapporlo ai 3 tasselli già posti, che ci permette di inserire altre 5 tasselli. Abbiamo quindi che il numero di tasselli (e di triangoli) sono numeri di Fibonacci: 1,3,5,8,.... Iterando il procedimento si ottiene una tassellatura del triangolo iniziale (A-tassellatura) che è non periodica, giacché in ogni passo abbiamo due insiemi:

le cui cardinalità sono numeri di Fibonacci, e il limite del rapporto tra due numeri di Fibonacci consecutivi è la sezione aurea φ. Diversamente, per una tassellatura periodica il limite del rapporto tra i numeri successivi di triangoli del tipo (+1) e (-1) deve essere razionale. Ne segue che l'A-tassellatura è aperiodica.

No TweetBacks yet. (Be the first to Tweet this post)