Le tassellature di Escher

Giugno 27th, 2021 | by Marcello Colozzo |

escher,tassellature,piastrellatura — **Fig. 1**

Assegnato lo spazio euclideo R² denotiamo con T una famiglia di sottoinsiemi di R²:

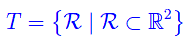
Definizione 1
T tassella debolmente R² se

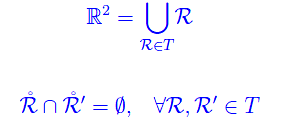
Definizione 2
T tassella R² se esiste una isometria del piano che trasforma R in R', per ogni R,R' appartenenti a T.

Definizione 3
T è una tassellatura periodica di R² se esiste una simmetria per traslazione rispetto a due direzioni indipendenti.

Nella arti visive, l'isometria di una tessellatura può anche essere realizzata per rotazione e per riflessione, come accade nelle litografie di Escher. Giocando sui contrasti di luce in modo da modulare la percezione dell'osservatore su "figura" e "sfondo", Escher cavalca alcune idee della psicologia della forma (Gestsalt) che caratterizzava gli ambienti degli intellettuali verso la fine degli anni Trenta. Un esempio è dato dalla xilografia Giorno e notte. In basso e al centro è ben visibile una tassellatura romboidale che viene modulata (alzando lo sguardo) per generare un mosaico piatto di uccelli bianchi e neri. Una successiva trasformazione aggiunge una dimensione restituendo due stormi di uccelli tridimensionali che volano in direzioni opposte. La comparsa della tridimensionalità è una conseguenza della trasformazione dello sfondo (Gestalt).

No TweetBacks yet. (Be the first to Tweet this post)