Tasso di contagio effettivo (Rt) e indice di positività
Maggio 8th, 2021 | by Marcello Colozzo |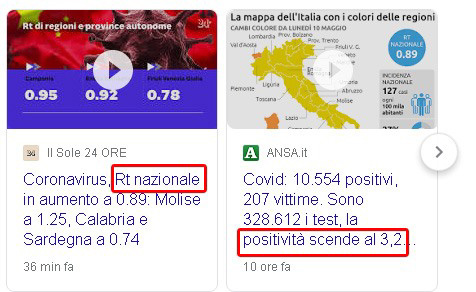
Teorema
Condizione sufficiente affinchè l'indice di positività sia una funzione monotonamente crescente, è che il tasso di contagio effettivo R(t) sia a sua volta una funzione monotonamente crescente.
La condizione non è necessaria: se R(t) è monotonamente decrescente, ciò non implica la medesima monotonia per l'indice di positività.
Dim.
In questo semplice modello epidemiologico la funzione y(t) enumera i contagi a partire dal paziente zero, matematicamente rappresentato dal valore iniziale normalizzato y(0)=1. Le nostre ipotesi su y(t) sono:
Definiamo il tasso di contagio effettivo
cioè il tasso di contagio è infinitesimo all'infinito, i.e. a ciclo pandemico concluso. Se nell'istante t vengono processati N(t) tamponi, possiamo definire l'indice di positività:
Ne segue
Facciamo le seguenti ipotesi:
che ci consentono l'ovvia approssimazione:
Derivando rispetto al tempo:per cui
onde
Viceversa
cioè
quindi l'asserto.




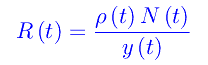
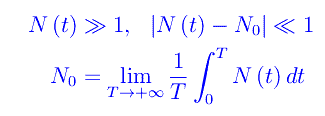
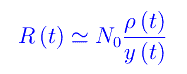







 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











