Le "onde anticipate" di Fantappiè

Aprile 23rd, 2021 | by Marcello Colozzo |

luigi fantappiè,sintropia,onde anticipate

Partiamo dall'equazione di D'Alembert 1-dimensionale scritta in forma operatoriale

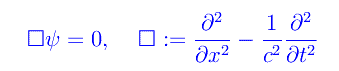
cosicché le soluzioni sono elementi del Kernel dell'operatore delambertiano, che nella rappresentazione spaziotemporale xt si scrivono

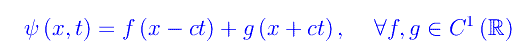
Fisicamente, la più generale soluzione dell'equazione di D'Alembert è una sovrapposizione lineare di un sistema di onde piane, di cui una è progressiva, l'altra regressiva. Una particolare classe di soluzioni è del tipo onda piana monocromatica, i.e. quando f (o g) è sinusoidale. In notazione complessa scriviamo

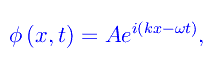
avendo introdotto il numero d'onde k e la frequenza angolare ω. La linearità dell'equazione di D'Alembert ci consente di sviluppare la soluzione generale in integrale di Fourier rispetto alla variabile tempo:

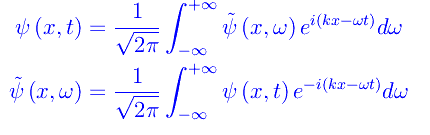
Imponendo che ψ(x,t) sia una soluzione, si trova una relazione tra ω e k, che non stiamo qui a ricavare. Il predetto sviluppo non fa altro che «decomporre» la soluzione ψ(x,t) in un componenti monocromatiche. Precisamente, la grandezza differenziale

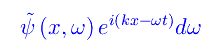
è l'ampiezza delle componenti monocromatiche di frequenza appartenenti all'intervallo infinitesimo [ω,ω+dω]. Si noti che l'integrazione va eseguita da -oo a +oo, cosicché si apre il fastidioso problema dell'interpretazione delle «frequenze negative». Incidentalmente lo spettro che cade in (-oo,0) non può essere ignorato, in quanto ciò violerebbe le ipotesi del teorema che sta alla base dello sviluppo di Fourier (qui c'entra la complicata nozione di «completezza» di un sistema di autofunzioni).

Nel 1943 il matematico italiano Luigi Fantappiè propose la seguente interpretazione delle onde a frequenza negativa: nell'integrale di Fourier procediamo per decomposizione

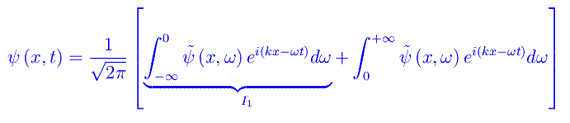
Nell'integrale I₁ eseguiamo il cambio di variabile ω'=-ω, per cui

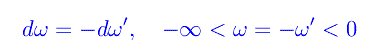
cosicché

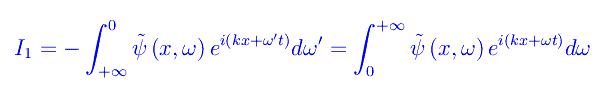
avendo rinominato omega;' in omega;, giacché si tratta di una variabile muta. Segue banalmente

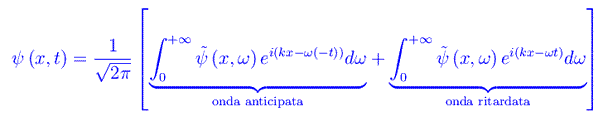
In altri termini, l'integrale generale della celebre equazione d'onda di D'Alembert si esprime come sovrapposizione lineare di una «onda ritardata» e di una «onda anticipata». Quest'ultima denominazione è legata al fatto che la predetta onda si propaga «indietro nel tempo».

No TweetBacks yet. (Be the first to Tweet this post)