Condizione necessaria e sufficiente affinché una curva sia una retta
Dicembre 15th, 2020 | by Marcello Colozzo |
Teorema
Condizione necessaria e sufficiente affinché la curva

sia una retta, è che la curvatura k(t) sia la funzione identicamente nulla.
Dim.
La condizione è sufficiente
Per ipotesi è k(t)=0, per ogni t reale. In funzione del parametro naturale s e con ovvio significato dei simboli:
che è la rappresentazione naturale di una retta.La condizione è necessaria
Per ipotesi γ è una retta, per cui una qualunque rappresentazione parametrica è
con a,b vettori costanti. Un vettore tangente è
Dal teorema precedente
Theorem
Necessary and sufficient condition for the curve

is a straight line, is that the curvature k (t) is the identically null function.
Proof
The condition is sufficient
By hypothesis it is k(t) = 0, for every real t. According to the natural parameter s and with obvious meaning of the symbols:
which is the natural representation of a straight line.
The condition is necessary
By hypothesis γ is a straight line, so any parametric representation is
with a, b constant vectors. A tangent vector is
From the previous theorem
Tags: Condizione necessaria e sufficiente affinché una curva sia una retta
Articoli correlati

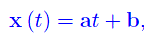
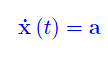
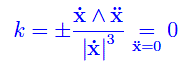


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











