» Esercizi svolti di Matematica e Fisica

Non invertibilità del Teorema di Lagrange

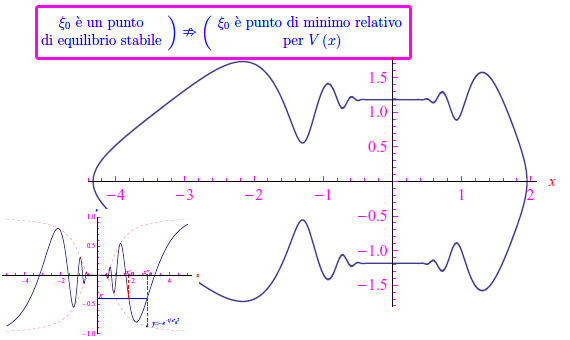
In precedenza, abbiamo dimostrato il Teorema di Lagrange che rappresenta un importante criterio per la stabilità (secondo Lyapunov) di una posizione di equilibrio per un sistema conservativo. Osserviamo tuttavia, che si tratta di una condizione sufficiente ma non necessaria. Il controesempio che proponiamo mostra infatti, l'esistenza di funzioni V(x) (energia potenziale) di classe C^oo ma non analitiche, le quali ammettono punti di equilibrio stabile ma che non sono di minimo relativo per V(x).
La condizione espressa dal teorema di Lagrange diviene necessaria e sufficiente, se si aggiunge l'ipotesi di analiticità dell'energia potenziale.

Per i dettagli matematici, scarica questo pdf

Tags: energia potenziale, posizioni di equilibrio stabile, teorema di lagrange