Campionamento di un segnale. Sampling (signal processing)
Ottobre 6th, 2020 | by Marcello Colozzo |
Consideriamo il seguente segnale deterministico (in unità adimensionali):

dove t0=0.8,τ=2.7. In fig.

riportiamo il grafico della funzione y(t). Eseguiamo una partizione dell'intervallo [t0,t0+&tau]:

essendo N un assegnato intero naturale > 1.
Definizione
La grandezza
si dice intervallo di campionamento.
Dobbiamo imporre

Ad esempio, per N=20 otteniamo il campionamento illustrato in fig. 1.
Di seguito il codice Mathematica per campionare un segnale.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: campionamento, sampling, segnale, signal processing
Articoli correlati
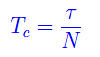


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











