Equilibrio di un sistema di pesi, di cui uno su piano inclinato |

Equilibrio di un sistema di pesi, di cui uno su piano inclinato

Luglio 5th, 2020 | by Marcello Colozzo |

statica,piano inclinato,equilibrio — **Fig. 1**

Esercizio tratto dal celebre Mandò, scritto in un campo di concentramento nazista. La soluzione è nostra

In fig. 1 P e Q sono due pesi collegati da una funicella, tramite la caccucola D; AC è un piano inclinaato, su cui appoggia il peso P.

Dati P e Q e l'inclinazione α del piano inclinato, (e trascurando tutti gli attriti) calcolare il valore dell'angolo θ (tra funicella e piano) per cui il sistema di pesi è in equilibrio.

Soluzione

Orientiamo un sistema di assi cartesiani ortogonali x,y come in fig. 2, dove sono riportate le forze agenti su P. Precisamente, il vettore P è la forza peso di P, mentre T e R_N sono rispettivamente la tensione della funicella e la reazione del piano inclinato.

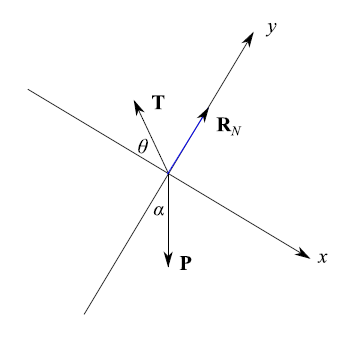
Deve essere:

che proiettata sui predetti assi cartesiani, fornisce il sistema di equazioni scalari:

Dalla prima

in cui compaiono le incognite T,θ. La seconda incognita è proprio quella chiesta dall'esercizio. Per svincolarci dalla tensione T, imponiamo la condizione di equilibrio per Q:

dove il vettore Q è la forza peso di Q. Si noti che compare la medesima tensione giacché si assume tacitamente trascurabile la massa della funicella. Orientando un asse η verso l'alto, si ha: