Traiettorie ortogonali

Maggio 28th, 2020 | by Marcello Colozzo |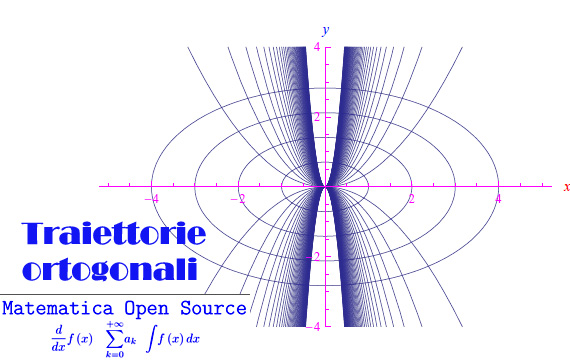

traiettorie ortogonali,equazioni differenziali
Fig. 1


Esercizio
Determinare le traiettorie ortogonali della seguente famiglia di curve piane:


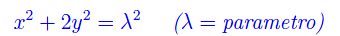
Soluzione

Definizione
Assegnata una F famiglia di curve piane, le traiettorie ortogonali di F famiglia costituiscono una famiglia


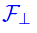
di curve piane, ciascuna delle quali interseca ogni curva di F secondo un angolo retto.


Se la famiglia assegnata è generata da un'equazione differenziale


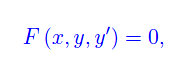
la famiglia delle traiettorie ortogonali è generata dall'equazione differenziale


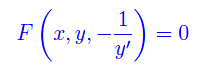
Ciò premesso, dobbiamo prima ricavare l'equazione differenziale che genera la famiglia di ellissi


A tale scopo deriviamo primo e secondo membro rispetto a x:


che è un'equazione differenziale del tipo


essendo F(x,y,y')=x+2yy'. Per quanto precede, l'equazione differenziale che genera le traiettorie ortogonali alla famiglia di ellissi è

Cioè


ovvero a variabili separabili. Integrando


che è la famiglia richiesta. In fig. 1 alcune curve di entrambe le famiglie.

No TweetBacks yet. (Be the first to Tweet this post)

Tags: ,

Articoli correlati

Commenta l'esercizio