» Esercizi svolti di Matematica e Fisica

Esercizio svolto sul metodo di variazione delle costanti arbitrarie (equazioni differenziali)

Maggio 25th, 2020 | by Marcello Colozzo |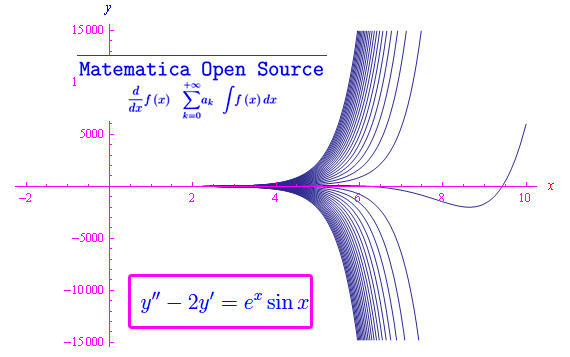

---

Assegnata l'equazione differenziale rappresentata in fig. 1, si determini un integrale particolare applicando il metodo di Lagrange

---

Soluzione
Dobbiamo innanzitutto trovare un sistema fondamentale di integrali dell'equazione omogenea

la cui equazione caratteristica

ammette una coppia di radici reali e distinte: λ₁=0,λ₂=2. Ne seguono gli integrali fondamentali:

Un integrale particolare della non omogenea è

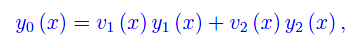
con v1(x),v2(x) tali che

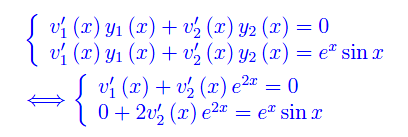
Il determinante della matrice dei coefficienti di tale sistema lineare è ovviamente il wronskiano dei predetti integrali fondamentali

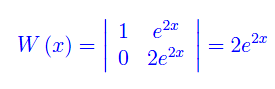
Applichiamo la regola di Cramer

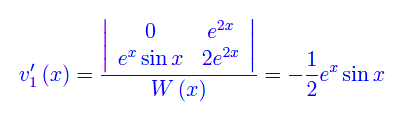
mentre l'altra incognita si ricava facilmente:

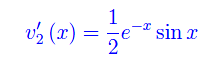
Non ci resta che eseguire una quadratura

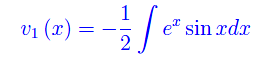
L'integrale a secondo membro si calcola facilmente per parti:

da cui

Quindi

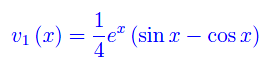
Passiamo all'altra funzione

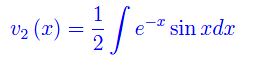
Procedimento simile al precedente:

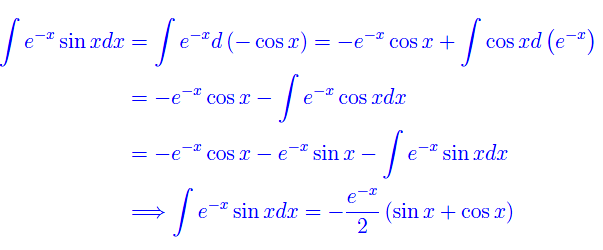
Perciò

Finalmente l'integrale particolare della non omogenea:

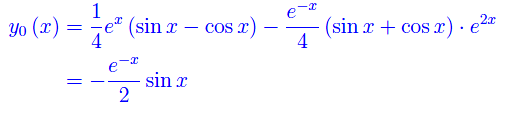
Ne concludiamo che l'integrale generale dell'equazione assegnata è

In fig. 1 l'andamento di alcune curve integrali della predetta equazione.

---

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: Equazioni differenziali, metodo di lagrange, metodo di variazione delle costanti arbitrarie

Articoli correlati