[¯|¯] Equazioni differenziali del tipo Bernoulli

Aprile 1st, 2020 | by Marcello Colozzo |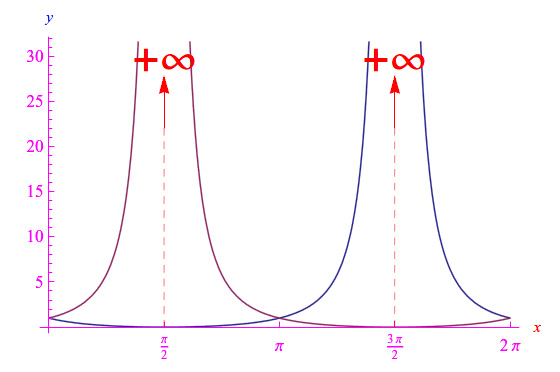

equazione di bernoulli,equazioni differenziali
Fig. 1


Un'equazione differenziale del tipo Bernoulli ha la forma:

dove n > 0 e α(x),ß(x) sono funzioni continue assegnate. Si noti che per n=1 l'equazione è lineare, per cui escludiamo questo caso. L'equazione può comunque essere ridotta a un'equazione lineare, attraverso il cambio di variabile:


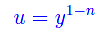
Infatti, calcolando


dopo qualche passaggio otteniamo


che è appunto lineare. Ad esempio, supponiamo di avere


Il cambio di variabile


Segue











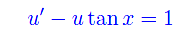
Il fattore integrante relativo a quest'ultima equazione è


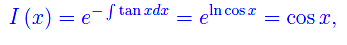
per cui

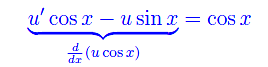
Integrando


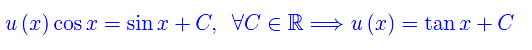
Ripristinando la variabile y, otteniamo l'integrale generale

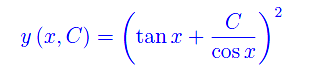
Osservazione
La funzione identicamente y(x)=0 nulla è un integrale dell'equazione assegnata. Tuttavia, non può essere ricavato dall'integrale generale. Ne concudiamo che è un integrale singolare.

Osserviamo infine che il problema di Cauchy:


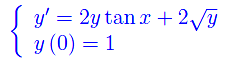
ammette due soluzioni distinte:

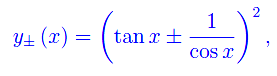
graficate in fig. 1.

No TweetBacks yet. (Be the first to Tweet this post)

Tags: ,

Articoli correlati

Commenta l'esercizio