» Esercizi svolti di Matematica e Fisica

[Nana bianca] Energia dello stato fondamentale del gas di elettroni relativistici

Febbraio 28th, 2020 | by Marcello Colozzo |

Per esplicitare questa condizione di equilibrio dobbiamo determinare separatamente l'energia E₀ e la self energia gravitazionale V_G(R). Iniziamo a determinare la prima grandezza.
Nel nostro modello abbiamo N elettroni nello stato fondamentale. Dal momento che il moto è relativistico, l'hamiltoniana di singola particella è

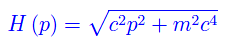
Si noti che non stiamo considerando campi esterni, giacché il campo gravitazionale è inglobato nel termine V_{G}(R) che poi andremo a calcolare separatamente. Abbiamo già calcolato in precedenza l'impulso di Fermi:

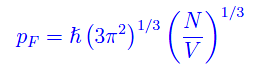
Segue

dove il fattore 2 è il peso statistico relativo al numero quantico di spin di singolo elettrone, cioè

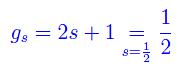
Se R definisce il bordo della configurazione di equilibrio, abbiamo che il suo volume è

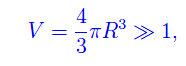
per cui lo spettro degli autovalori dell'impulso compongono uno spettro quasi-continuo. Quindi:

Passando alle coordinate sferiche nello spazio degli impulsi:

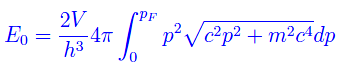
Eseguiamo il cambio di variabile

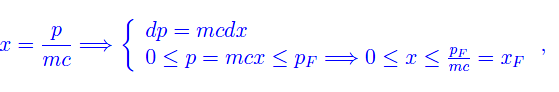
onde

che può essere espresso come:

dove

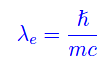
è la lunghezza d'onda Compton dell'elettrone. In definitiva, l'energia E₀ diventa:

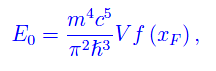
dove

è il cosiddetto integrale di Fermi

Tale risultato implica che la condizione di equilibrio è

Tags: gas di elettroni relativistici degenere, impulso di fermi, nana bianca

Articoli correlati