[¯|¯] Disequazioni razionali fratte

Gennaio 24th, 2020 | by Marcello Colozzo |

Disequazioni razionali fratte
(Esercizi tratti dal Zwirner --Analisi matematica 1. La soluzione è nostra).
Esercizio 1
Risolvere la disequazione

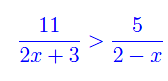
Portiamo tutto a primo membro:

Quindi

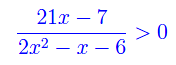
Dobbiamo quindi studiare il segno del rapporto appena scritto. Studiamo prima il segno di numeratore e denominatore:

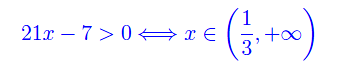
Per il denominatore dopo aver trovato le radici -3/2, 2 della corrispondente equazione, si ha

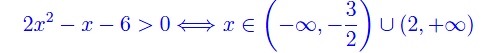
A questo punto applichiamo un procedimento grafico che è più spedito al procedimento analitico che consiste nel risolvere i corrispondenti sistemi di disequazioni (una volta per il segno positivo, un'altra per il segno negativo). Precisamente, guardiamo il grafico di fig.

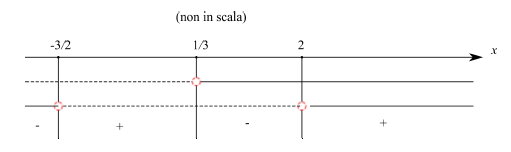
Le linee continue rappresentano il segno (+), mentre quelle in tratteggio il segno (-), per cui sono giustificati gli altri segni ± che compaiono più sotto. Ed è chiaro che questi sono proprio i segni che stiamo cercando. I cerchietti rossi ci dicono che quel punto (i.e. numero sulla retta reale) va escluso. Diversamente, si inserisce un pallino nero.
L'insieme delle soluzioni è

Esercizio 2
Per quali valori del parametro reale m l'equazione

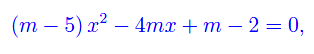
ammette radici reali e di ugual segno?

Soluzione
Per la realtà delle radici dobbiamo imporre la non negatività del discriminante:

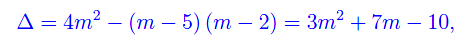
onde

Al solito, calcoliamo prima le radici dell'equazione corrispondente, ottenendo m₁=-10/3, m₂=1. Quindi

Calcoliamo ora le radici dell'equazione assegnata:

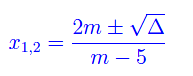
L'esercizio dice che devono avere lo stesso segno, quindi

La seconda condizione è quindi rappresentata dallo studio del segno del rapporto ((m-2)/(m-5)), in particolare dobbiamo vedere per quali m è positivo. Costriamo il grafico di fig.

per poi giungere a

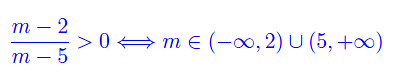
A questo punto risolviamo il sistema di disequazioni

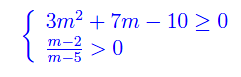
Siccome già conosciamo le soluzioni, non dobbiamo fare altro che costruire il grafico di fig. 1. Conclusione: l'equazione assegnata ammette radici reali e di ugual segno per tutti e soli i valori del parametro reale m appartenente all'insieme: