[¯|¯] La formula di Nielsen-Ramanujan

Settembre 28th, 2019 | by Marcello Colozzo |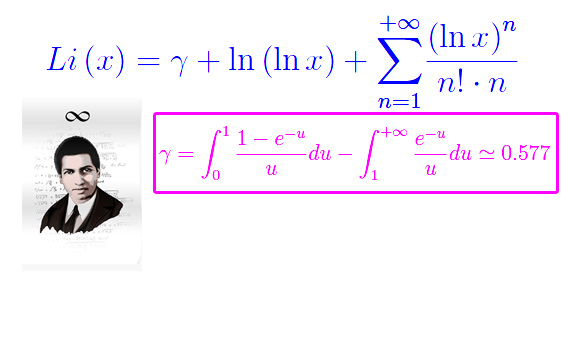

Probabilmente il numero di zeri della zeta di Riemann non appartenenti alla retta critica (dimostrando per assurdo la congettura di Riemann), non giocano alcun ruolo sul comportamento asintotico della distribuzione dei primi (regolato dal Teorema dei numeri primi). La ragione è da ricercarsi nel fatto che il predetto comportamento è deterministicamente assegnato dalle proprietà della funzione logaritmo integrale che nello sviluppo in serie trovato da Riemann, rappresenta il contributo dominante. Più precisamente, gli zeri della funzione zeta hanno un "effetto locale" ovvero in un appropriato intorno di un assegnato numero primo (preso ad arbitrio).
In ogni caso, è preferibile approfondire il comportamento del suddetto termine dominante, ovvero del logaritmo integrale.

Scarica il file pdf

No TweetBacks yet. (Be the first to Tweet this post)