[¯|¯] Spazi di prodotto scalare. Spazi euclidei

Marzo 29th, 2019 | by Marcello Colozzo |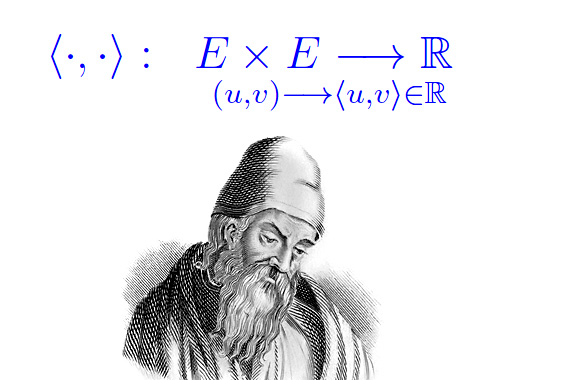

spazi di prodotto scalare,prodotto scalare,spazi euclidei

Definizione
Un qualunque spazio vettoriale V sul campo reale si dice spazio vettoriale reale.
Un qualunque spazio vettoriale V sul campo reale si dice spazio vettoriale complesso.
Osserviamo che nozioni quali ortogonalità e lunghezza non compaiono in un generico spazio vettoriale (reale o complesso). Per introdurre tali nozioni, dobbiamo definire un nuovo ente denominato prodotto scalare. A tale scopo distinguiamo il caso reale da quello complesso.

Spazi vettoriali euclidei

Definizione
Uno spazio vettoriale euclideo è uno spazio vettoriale reale che indichiamo con E, in cui è definito un prodotto scalare ovvero un'applicazione:

che verifica le seguenti proprietà

Proprietà commutativa

Proprietà associativa rispetto alla moltiplicazione di uno scalare per un vettore

Proprietà distributiva rispetto all'addizione vettoriale

Le proprietà 1,2,3 implicano che il prodotto scalare è una forma bilineare definita in E×E (cioè lineare rispetto a ogni vettore) e simmetrica.
Esempio
Nello spazio vettoriale Rⁿ, definiamo l'applicazione

che è manifestamente un prodotto scalare. Ne consegue che con l'applicazione appena definita, Rⁿ assume la struttura di spazio euclideo.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.