[¯|¯] Una condizione necessaria e sufficiente per la sommabilità di una funzione
Febbraio 21st, 2019 | by Marcello Colozzo |
Per quanto stabilito nei numeri precedenti, una funzione generalmente continua in un intervallo X (limitato o illimitato), si dice integrabile se è possibile determinare univocamente l'ente denominato integrale generalizzato

che sia in grado di inglobare la definizione di integrale definito. Si noti che

Nel caso particolare
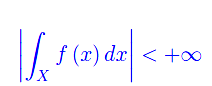
diremo che f è sommabile in X. Ne consegue che la sommabilità di una funzione è una condizione più forte dell'integrabilità. Il seguente teorema esprime una condizione necessaria e sufficiente per la sommabilità di una funzione:
Teorema

Dim.
La condizione è sufficiente
Dopo aver introdotto le solite funzioni non negative
prendiamo ad arbitrio
Segue
Dalle formule scritte più sopra
Per ipotesi f(x) è sommabile in X, per cui tali saranno le fk(x):
Segue
Cioè
Segue
essendo
Ma
onde l'asserto.La sufficienza della condizione è lasciata per esercizio.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

No TweetBacks yet. (Be the first to Tweet this post)
Tags: condizione necessaria e sufficiente, integrabilità, sommabilità
Articoli correlati


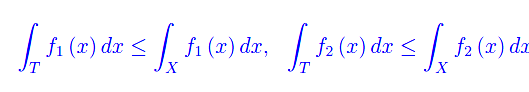


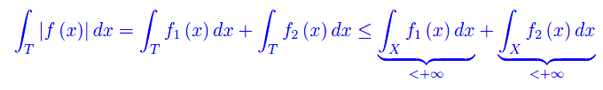



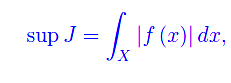



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









