» Esercizi svolti di Matematica e Fisica

[¯|¯] (PARTE 2) Il barcaiolo matematico e le equazioni differenziali

Novembre 4th, 2018 | by Marcello Colozzo |

Riprendiamo il il problema della barca del post precedente, dove avevamo considerato un corrente che genera un campo di forze con componente secondo l'asse x pari a una costante. Cosa succede, invece, se tale componente cresce linearmente con la distanza della sponda di partenza? Per rispondere al quesito non dobbiamo fare altro che riprendere il sistema di equazioni differenziali del moto:

con K₁ costante di integrazione. Integrando nuovamente abbiamo l'integrale generale:

Applicando le condizioni iniziali, si ottiene:

Quindi le equazioni orarie del moto sono:

Tali equazioni costituiscono una rappresentazione parametrica della traiettoria. Eliminando il parametro t, otteniamo:

ovvero

Determiniamo le coordinate cartesiane del punto d'approdo:

Pertanto

come illustrato nella fig. al top. Tale risultato sembra anti-intuitivo poiché ci aspettiamo una traiettoria con una pendenza minore rispetto a quella del caso con forza costante. Tuttavia nel caso attuale la componente F_x della forza è nulla per x=0. Inoltre, l'ascissa del punto di approdo Q pur dipendendo da d³ (mentre nel caso 2 dipende da d²), contiene il parametro k. Confrontando le ascisse di Q nei casi predetti, si ha:

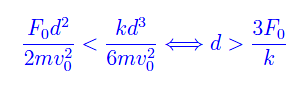
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: barcaiolo, Equazioni differenziali, matematico

Articoli correlati