[¯|¯] Piano osculatore alla cubica sghemba

Settembre 27th, 2017 | by Marcello Colozzo |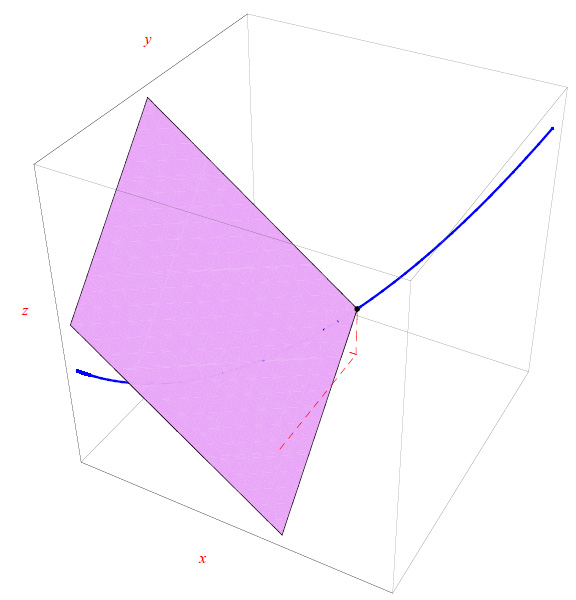

piano osculatore,cerchio osculatore,cubica sghemba

Nel post precedente abbiamo esaminato la nozione di piano osculatore e cerchio osculatore ad una assegnata curva regolare. Vediamo ora un esempio numerico offerto dalla determinazione del piano osculatore alla cubica sghemba:

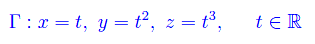
mostrando che in ogni punto (x,y,z) il piano osculatore stacca sugli assi coordinati tre segmenti di lunghezza (x/3),-(y/3),z.

Preso ad arbitrio t_{0sub> nell'intervallo base, l'equazione del piano osculatore a Γ nel punto (t₀,t₀²,t₀³) è:}

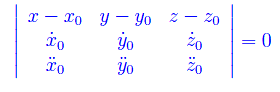
Nel caso in esame è

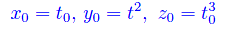
Per calcolare i rimanenti elementi del determinante a primo membro valutiamo le derivate delle funzioni x(t),y(t),z(t):

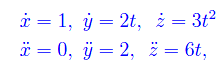
per cui

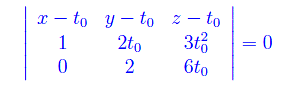
Sviluppando il determinante secondo gli elementi della prima riga, si trova

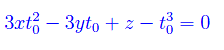
In virtù dell'arbitrarietà di t₀, l'equazione precedente può essere riscritta come

continua in pdf

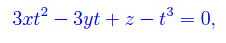
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

No TweetBacks yet. (Be the first to Tweet this post)