» Esercizi svolti di Matematica e Fisica

[¯|¯] Sistema di coordinate in co-moving

I dati osservativi ci dicono che per distanze superiori ai 100 Mpc, l'universo è omogeneo ed isotropo: non esistono posizioni e direzioni privilegiate per ciò che riguarda le proprietà fisiche.

La struttura a larga scala dell'universo è governata dalla teoria della Relatività Generale di Einstein; scriviamo quindi le equazioni di campo di Einstein senza il termine cosmologico:

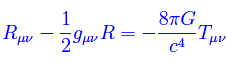
Ricordiamo che g_µν, R_µν, R, sono rispettivamente il tensore metrico, il tensore di Ricci, lo scalare di curvatura, mentre T_µν è il tensore energia-impulso della materia in una sua rappresentazione fenomenologica. Tali equazioni ammettono una classe di soluzioni dotate della suddetta simmetria. Soluzioni note come modelli di Friedmann, mentre la richiesta di omogeneità ed isotropia è nota come Principio Cosmologico.

In Relatività Generale la scelta del sistema di coordinate è totalmente arbitraria, e nella ricerca delle soluzioni di Friedmann, il sistema di coordinate più idoneo è quello in co-moving.

Iniziamo col modellizzare la materia che riempie l'universo attraverso un fluido, il cui singolo elemento è individuato da tre coordinate spaziali x^k.

Le particelle del fluido sono in caduta libera nel campo gravitazionale di fondo dell'universo, e tali saranno i punti coordinati del riferimento in co-moving. Quindi, l'intervallo coordinato tra una coppia qualsiasi di particelle rimane costante, e l'espansione o la contrazione dell'universo è dovuta a un cambiamento della metrica dello spazio-tempo. Utilizziamo come coordinata temporale x°=ct il tempo proprio misurato da un orologio trasportato dalle particelle del fluido. Si ricordi che l'intervallo di tempo proprio tra due eventi infinitamente vicini P(x°,x^k) e P+dP(x°+dx°,x^k+dx^k) è dato da:

continua in pdf

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: sistema di coordinate in co-moving, sostema di coordinate sincrono