[¯|¯] Un efficace algoritmo per risolvere la forma indeterminata 1oo
Febbraio 7th, 2017 | by Marcello Colozzo |
Proponiamo un algoritmo per risolvere la forma indeterminata 1oo. Assumiamo
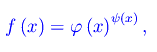
con
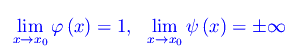
Segue
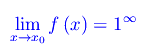
Osserviamo che
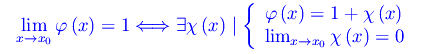
Cioè la funzione φ(x) converge a 1 per x->x0, se e solo se esiste una funzione χ(x) infinitesima in x=x0. Con tale posizione il limite si scrive:
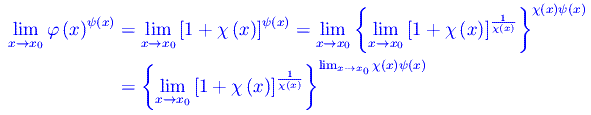
Calcoliamo il primo limite con il cambio di variabile
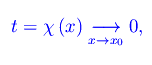
per cui
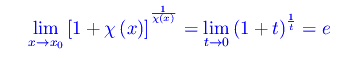
Finalmente:
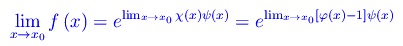
Applichiamo questo procedimento al limite dell'esempio precedente:
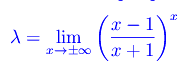
Qui è
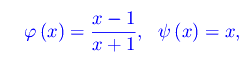
onde
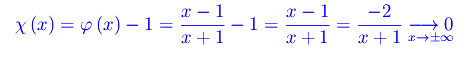
Pertanto
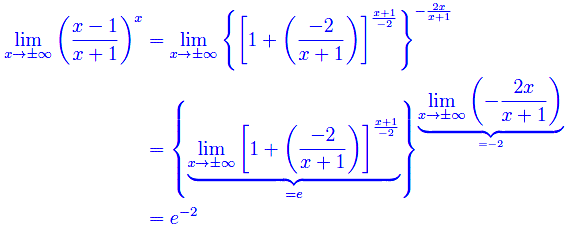
Dall'esecuzione dei calcoli vediamo che l'algoritmo proposto ha un costo computazionale più alto di quello utilizzato nel predetto esempio. È tuttavia vantaggioso nei casi in cui il limite è più complicato.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: algoritmo, forma indeterminata 1 elevato a infinito, limiti di funzioni esponenziali
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











