» Esercizi svolti di Matematica e Fisica

[¯|¯] Il gioco degli scacchi, Mathematica e l'Algoritmo di Elo generalizzato

Cos'è l'algoritmo di Elo?

È ben spiegato su Wikipedia. Arpad Emrick Elo era un fisico ungherese e campione di scacchi. Scrisse il famoso algoritmo che permette di computare le "aspettative" (o probabilità) di vittoria per una coppia di giocatori (A,B). Le probabilità si calcolano in funzione alla differenza di forza relativa o punteggio (ranking) di singolo giocatore. Più precisamente:

Pa = (1+10^(Rb-Ra)/400)^-1

dove Pa è la probabilità di vittoria per A. Qui Ra e Rb sono i punteggi di A e B. La probabilità per B è ovviamente:

Pb = 1-Pa = (1+10^(Ra-Rb)/400)^-1

Questo formule sono date ad hoc e se tracciamo i grafici, riusciamo a capire che sono ragionevoli. Sono noti Ra e Rb, per cui le formule ci permettono di calcolare le probabilità. L'algoritmo di Elo è basato sulla regola di aggiornamento dei punteggi di A e B. Più precisamente, A e B eseguono N partite. Si parte dalla partita 0 con punteggi noti e si aggiornano secondo la regola riportata su wikipedia. Ad esempio, se A ha una bassa probabilità ma, comunque, riesce a vincere, allora il suo punteggio avrà un buon incremento. Viceversa, se perde pur avendo un'alta probabilità. Facendo alcuni passaggi si ottiene che la (k+1)-esima probabilità si esprime attraverso la k-esima probabilità. In breve, abbiamo un processo ricorsivo, ovvero un sistema dinamico iterato, cioè una black box che accetta un input x_k=probabilità k-esima e, in base a una funzione di trasferimento f(x), emette un output x_(k+1)=
probabilità (k+1)-esima.

Possiamo modificare l'algoritmo in modo da applicarlo a un qualunque gioco a somma zero G. Le probabilità sono:

Pa = (1+e^b(Rb-Ra))^-1

e Pb=1-Pa

Qui b è un fattore di scala. Ora Ra e Rb vanno da -oo a +oo, e ciò permette di definire:

L'algoritmo è indeterminato quando A e B sono entrambi infinitamente forti o infinatamente deboli. Escludendo questi casi estremi si perviene a una Sistema dinamico iterato con funzione di trasferimento:

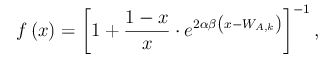
Qui W_a,k è un parametro che controlla l'esito della partita.

W_a,k = 1 se A vince la k-esima partita

W_a,k =0 altrimenti

Abbiamo, dunque, tutti gli ingredienti per implementare una simulazione con Mathematica, studiando il diagramma delle orbite e l'eventuale presenza di caos deterministico. C'è però un problema: ho dato in pasto a Mathematica il parametro W attraverso un pseudo random in {0,1}:

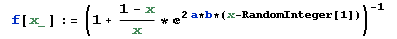
Ecco il risultato con una probabilità iniziale per A pari a 0.8:

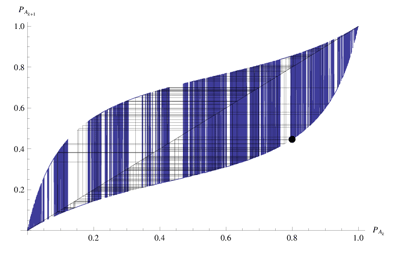
Per maggiori dettagli, scarica il pdf al link seguente:
Algoritmo di Elo.

Tags: algoritmo di Elo, scacchi