[¯|¯] Potenziale vettore. Campi solenoidali

Novembre 16th, 2019 | by Marcello Colozzo |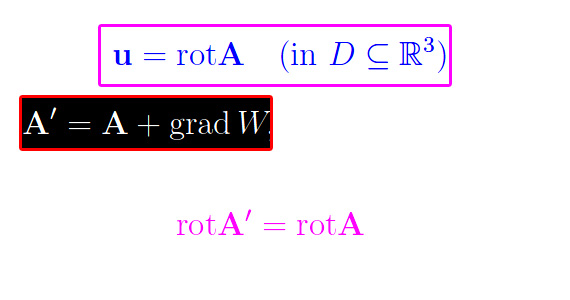

potenziale vettore, campo solenoidale, divergenza nulla — **Fig. 1**

Nella lezione precedente abbiamo stabilito l'importante nozione di campo conservativo. Ricordiamo velocemente che si tratta di un campo vettoriale che deriva da un potenziale scalare U(x,y,z), i.e. u = grad(U). Una condizione necessaria è l'irrotazionalità del campo, mentre una condizione sufficiente è la connessione lineare semplice del campo di esistenza: ogni curva generalmente regolare chiusa, è il bordo di una superficie generalmente regolare, aperta e contenuta nel predetto campo.

Se in luogo dell'equazione vettoriale u = grad(U) si considera quest'altra equazione u = rot(A), ci imbattiamo in una nuova classe di campi vettoriali: quelli derivanti da un potenziale vettore A(x,y,z). Notiamo una certa analogia con il caso precedente, cioè del potenziale scalare, nel senso che qui una condizione necessaria è data dall'annullarsi della divergenza (campo solenoidale), mentre una condizione sufficiente si identifica ancora una volta con la topologia del campo, che dovrà essere a connessione lineare semplice.
Un'ulteriore analogia: il potenziale scalare è definito a meno di una costante additiva arbitraria; il potenziale vettore è definito a meno del gradiente di un campo scalare arbitrario.

Scarica la lezione in pdf

No TweetBacks yet. (Be the first to Tweet this post)