» Esercizi svolti di Matematica e Fisica

[¯|¯] I sistemi formali e il Buddhismo Zen

v

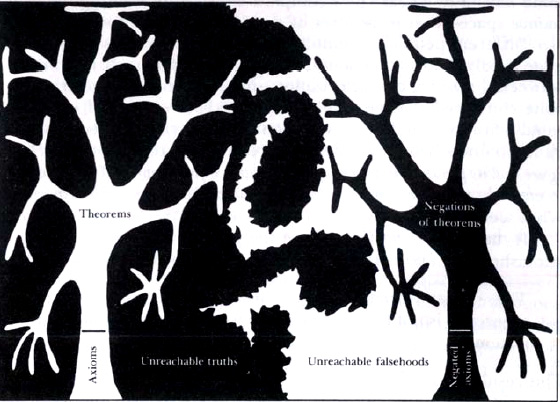
L'immagine di fig. 1 è tratta dal libro Gödel, Escher, Bach, un'eterna ghirlanda brillanate. Nell'articolo precedente abbiamo accennato ai sistemi formali e al Teorema di Gödel.

Soffermiamoci un attimo su una connessione inattesa tra la logica matematica e il Buddhismo Zen, come evidenziato dal libro citato. Si noti che ciò non viene presentato esplicitamente dall'autore, ma in due capitoli diversi. D'altra parte, lo scopo di questi articoli è quello di facilitare la lettura di Hoftsdater.

La fig. 1 metaforizza la genesi dei teoremi. Si parte dagli assiomi (radici di un albero), e attraverso un procedimento logico si dimostrano i teoremi, rappresentati dai rami dell'albero. L'immagine a destra è la parte speculare di quella a sinistra, ma l'aspetto interessante è l'esistenza di zone scoperte ovvero di "verità irraggiungibili" da quell'assegnato sistema formale. Un risultato analogo lo troviamo in un Koan zen del maestro spirituale Nansen. Scrive Hoftsdater

Lo Zen riconosce i suoi limiti, proprio come i matematici hanno imparato a riconoscere i limiti del metodo assiomatico come metodo per giungere alla verità.
[...]
Una delle affermazioni Zen più chiare sui confini dello Zen si ha nel seguente strano koan, che rientra moltissimo nello spirito di Nansen:
Tozan chiese ai suoi monaci: "Voi monaci dovreste sapere che c'è una conoscenza ancora più alta nel Buddhismo". Un monaco si fece avanti e chiese: "Quale è il Buddhismo più alto?". Tozan rispose: "Non è Buddha".
Lo Zen è un sistema, e non può essere il suo metasistema; c'è sempre qualcosa fuori dello Zen, che non può essere pienamente capito o descritto all'interno dello zen.

Tags: hoftsdater, Kurt Gödel, zen