[¯|¯] Tensori controvarianti
Giugno 4th, 2017 | by Marcello Colozzo |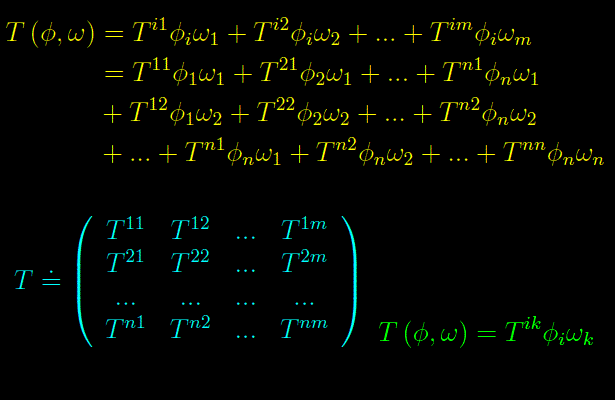
Siano En e Fm due spazi vettoriali sul medesimo campo K. Denotando con En* e Fm* i rispettivi spazi duali, consideriamo un'applicazione bilineare:
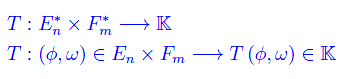
La bilinearità implica che T è un'applicazione additiva ed omogenea rispetto a φ, ω. Cioè
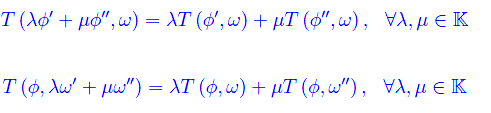
Definizione
La forma bilineare
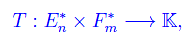
si dice tensore controvariante di rango 2 relativo agli spazi vettoriali En e Fm.
No TweetBacks yet. (Be the first to Tweet this post)
Tags: Forme bilineari, prodotto tensoriale, tensori controvarianti
Articoli correlati
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
