La propagazione di un virus può essere rappresentata da una funzione N(t) che esprime il numero di individui infetti nel generico istante t (i cosiddetti attualmente positivi). Più precisamente, tale propagazione è modellizzata da un sistema dinamico a tempo continuo:
dove f(t,N) è una funzione reale delle variabili reali t,N. Assumiamo tale funzione sufficientemente regolare in modo che siano verificate le ipotesi del Teorema di Cauchy-Lipschitz.
In un modello realistico, la predetta funzione si esprime come somma di due contributi:
Tipicamente ma non necessariamente, tale evoluzione è di tipo esponenziale:
cosicché per ffarm(t,N)=0 (identicamente), riesce
cioè una crescita esponenziale con costante di tempo τ=α-1. È chiaro allora che ffarm(t,N) modellizza un'azione di contenimento nei confronti della crescita incontrollata del virus (farmaci, quarantena, etc.). Si apre, quindi, il problema di scrivere una qualche espressione analitica per ffarm(t,N). Ad esempio, possiamo contemplare un modello in cui tale funzione si fattorizza nel prodotto di due termini:
dove λ > 1 è una costante che rende nonlineare (in N) il processo che stiamo studiando. Un caso speciale è il seguente:
Ne consegue che il problema di Cauchy inizialmente impostato diviene
la cui unica soluzione è
cioè N(t) decresce esponenzialmente con costante di tempo τ=α-1. Dobbiamo escludere questo caso ideale poiché non sappiamo come realizzare un'azione di contenimento stazionaria e caratterizzata da quel particolare valore (pari al doppio del reciproco della costante di tempo della crescita virale, cambiata di segno).
Viceversa, una azione di contenimento è tutt'altro che stazionaria, e in uno scenario realistico ci si aspetta un comportamento aleatorio. Ciò suggerisce di modellizzare ß(t) attraverso una opportuna variabile aleatoria. Consideriamo in particolare, un processo di Wiener i.e. l'integrale di un white noise W(t). Come è noto, quest'ultimo ha uno spettro di potenza piatto:
Dal Teorema di Wiener-Khintchine segue che la funzione di autocorrelazione è deltiforme:
In altri termini, i valori assunti da W(t) sono scorrelati al 100%. Per quanto precede, un processo di Wiener (noto anche come Brown noise) è un integrale di W(t). Con abuso di notazione, scriviamo:
L'abuso deriva dal fatto che la grandezza W(t) non è una funzione nel senso dell'analisi matematica. Tuttavia, il software Mathematica offre la possibilità di manipolare tali oggetti alla stregua delle usuali funzioni. Precisamente, dopo aver generato un array dei valori assunti da W(t) per un assegnato range di valori assunti da t, utilizziamo l'istruzione Interpolation[] per creare una funzione reale della variabile reale t, simboleggiata da
dopodichè calcoliamo una sua primitiva attraverso l'usuale istruzione Integrate[]. In simboli:
Il risultato è riportato in figura
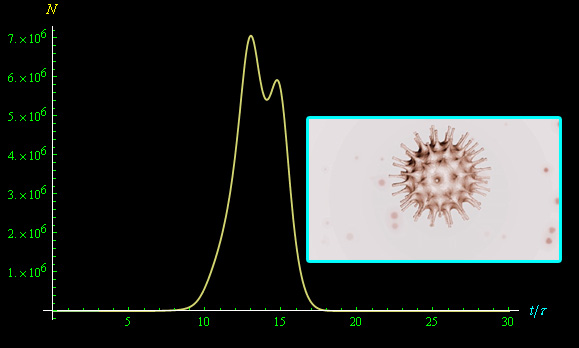
La grandezza ßint[t] deve essere introdotta nell'equazione differenziale che stiamo cercando di risolvere, e che va integrata numericamente con Mathematica. Ad esempio, con una particolare scelta dei parametri, il predetto script di Mathematica restituisce l'andamento (è ancora un modello molto rozzo!) plottato in fig. 1.