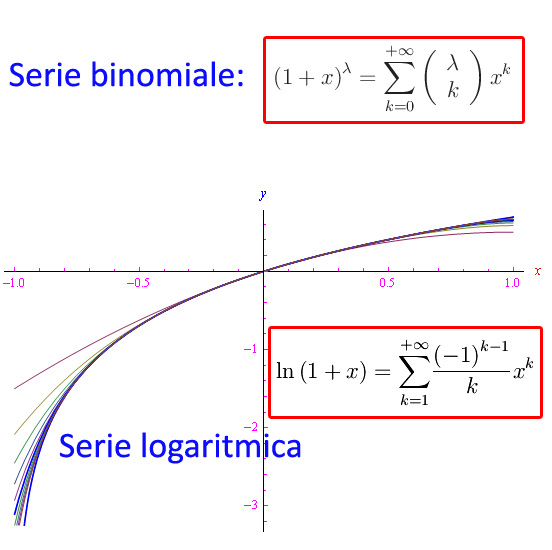
Serie logaritmica
È la serie di Mac-Laurin relativa alla funzione f(x)=ln(1+x). Tale funzione è definita in (-1,+8). Calcolando le derivate si trova:
Enunciamo senza dimostrare, il seguente
Teorema
La serie logaritmica converge assolutamente in (-1,1):
Serie binomiale
È la serie di Mac-Laurin relativa alla funzione potenza di esponente reale scritta come
Calcolando le derivate, si perviene a
Il generico termine ci ricorda il coefficiente binomiale di indice n e base k
ricordando che la convenzione 0!=1 implica:
Segue
che ci consente di estendere tale sviluppo al campo reale:
In tal modo, la precedente serie di Mac-Laurin assume la forma compatta:
Si tratta, dunque, di stabilire:
Osserviamo incidentalmente che nel caso di esponente intero naturale n:
Cioè la predetta serie si riduce a una somma di ordine n, restituendo la ben nota formua del binomio di Newton, valida per ogni x reale. Escludendo questo caso banale, enunciamo senza dimostrare il seguente
Teorema
La serie binomiale converge assolutamente in (-1,1):
Non converge per |x| > 1. Può al più convergere in [-1,1], trattando con le dovute cautele il punto x=-1, giacché le derivate di ordine k > λ non sono ivi definite, per cui non è applicabile il teorema dimostrato in questa lezione