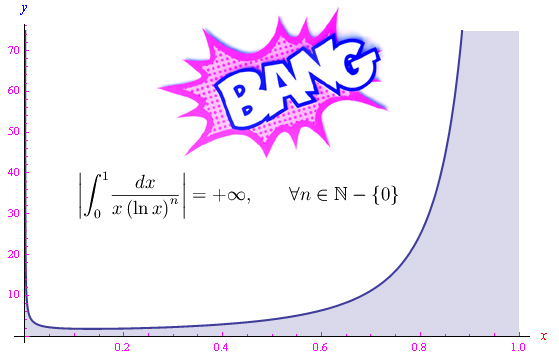
La funzione integranda dell'integrale generalizzato che proponiamo oggi dipende parametricamente da un intero naturale n non nullo. Applicando noti criteri di sommabilità (i.e. di convergenza) scopriamo che tale integrale diverge per ogni n non nullo (per inciso, anche per n=0, giacchè in tal caso l'integranda è un infinito di ordine 1 per x->0).
La funzione integranda risulta, tuttavia, integrabile. (Ricordiamo che una funzione è integrabile in un intervallo X se l'integrale esteso a X esiste. Se è finito, la funzione si dice sommabile. Se invece è infinito, allora la funzione è integrabile).
L'integrabilità della funzione assegnata deriva dal fatto che detta funzione ha segno costante nell'intervallo di integrazione [0,1].
Per i dettagli scarica l'esercizio in formato pdf.
No TweetBacks yet. (Be the first to Tweet this post)