Esercizio
Dimostrare che i punti P,Q,R sono allineati (fig. 1).
Soluzione
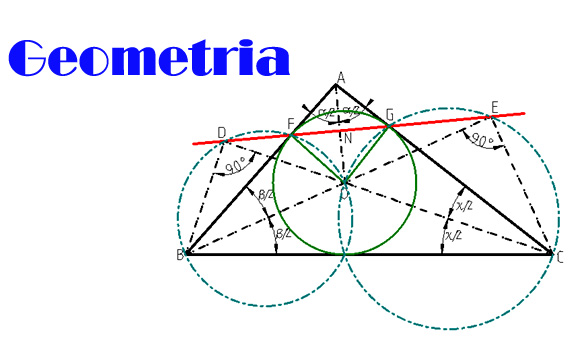
Dato un triangolo generico ABC siano α,ß,χ gli angoli corrispondenti ai vertici.(fig. 1). Si traccino le bisettrici da ogni vertice, le quali si incontreranno in O. Dal centro O si tracci la perpendicolare ad AB e ad AC. Disegnato il cerchio inscritto si ha FO=GO e AF=AG, pertanto AO è perpendicolare a FG nel punto N. Esaminiamo le bisettrici da B e da C. Si ha con ovvio significato dei simboli:
Poichè l'angolo BOD è supplementare all'angolo BOC, si ha
Ma l'angolo DBO è complementare a BOD, quindi
Poiché
si ha
Gli angoli in F e in D sono retti, quindi il quadrilatero BDFO è ciclico. Si ha
Nel triangolo DFB abbiamo
Poiché AFB è un segmento diritto e
per cui i punti D,F,G risultano allineati. In modo analogo si prova che E,G,F sono allineati. Pertanto D,F,G,E sono allineati.
No TweetBacks yet. (Be the first to Tweet this post)