Supponiamo di avere
nel senso che vogliamo determinare la più generale primitiva di e^φ(x) per una assegnata funzione continua φ(x) Forziamo la soluzione dell'equazione appena scritta:
con y(x) funzione incognita. Derivando primo e secondo membro
Per definizione di primitiva
che confrontata con la precedente, porge
che a sua volta è un'equazione differenziale lineare del primo ordine in y(x). Applichiamo il procedimento standard che consiste nel moltiplicare primo e secondo membro per un fattore integrante, che in questo caso è
onde
Integrando primo e secondo membro rispetto a x
cioè
Sostituendo nell'equazione scritta più sopra
Ad esempio, supponiamo di avere
Riesce
con y(x) soluzione di
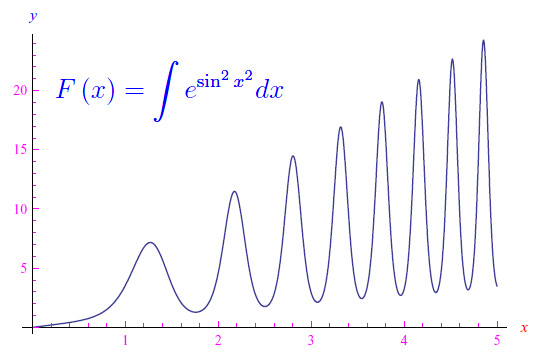
che può essere risolta numericamente con Mathematica. In definitiva otteniamo il grafico di una delle primitive (fig. 1).
Sostienici
Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
No TweetBacks yet. (Be the first to Tweet this post)