[¯|¯] Massima altezza di un gigante

Schematizziamo un organismo vivente Ω di altezza H attraverso un dominio D_H dello spazio euclideo tridimensionale. La massa inerziale di Ω è:

essendo ρ(x) la densità.

L'integrità di Ω è garantita dalle forze di coesione che tengono uniti gli atomi della sua superficie. Denotiamo con n_H(x) la densità del numero di coppie di atomi sulla superficie:

Se ε₀ > 0 è l'energia di interazione tra coppie di atomi che per quanto detto, assicurano la non frammentazione di Ω, si ha che l'energia totale di coesione è

esssendo

ovvero il numero di coppie di atomi sulla predetta superficie. D'altra parte se Ω cammina o corre, la sua energia meccanica è

dove v è il modulo della velocità del baricentro di Ω, mentre V=m(H)gH è l'energia potenziale gravitazionale. Quindi:

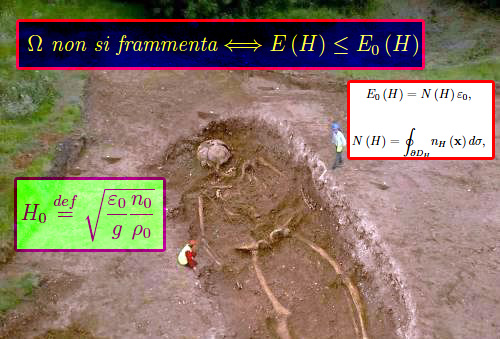
Segue manifestamente la condizione:

Condizione di non frammentazione

Prima di esplicitare tale condizione, assumiamo

cioè indipendenti da x,y,z. Inoltre

Quindi

da cui

Abbiamo

essendo

Si noti che

onde deve essere H < H₀, poiché nel caso contrario Ω non può muoversi senza frammentarsi. Valori tipici

mentre g=980cm/s^2. Quindi, nelle appropriate unità di misura

Risolvendo rispetto a n₀:

da cui vediamo che la densità del numero di atomi della superficie di Ω, è proporzionale al quadrato della massima altezza H₀.