[¯|¯] Separazione di variabili e integrali costanti

Integrare l'equazione differenziale:

Soluzione
Scriviamo l'equazione in forma normale

vediamo immediatamente che è a variabili separabili. Prima di separare le variabili, determiniamo gli eventuali integrali costanti. Deve essere

per cui

sono gli integrali costanti dell'equazione assegnata. Separando le variabili e integrando

Segue

Definendo una nuova costante di integrazione C=e^-2C₁, si ha

Prenendo C tale che C(y²-1)>0 l'equazione precedente si scrive:

da cui l'integrale generale

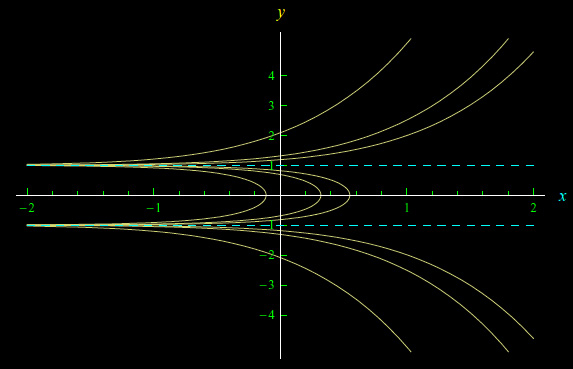
che per |C|->+oo riproduce gli integrali costanti y=±1.

Sostienici