Esercizio finalizzato al calcolo della densità spettrale del campo elettromagnetico emesso da una antenna
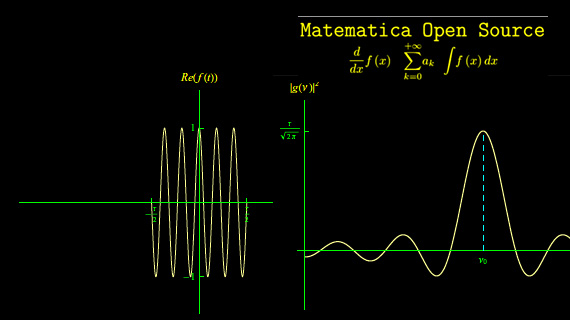
Determiniamo la trasformata di Fourier della seguente funzione (il grafico della parte reale è in fig. 1):
Iniziamo ad osservare che per avere una funzione continua sui bordi, dobbiamo considerare ν0 e τ legati da una qualche relazione. Per essere più specifici e prendendo la parte reale della funzione, dobbiamo avere:
che è verificata, ad esempio, per
Ciò premesso, la trasformata di Fourier della funzione assegnata è
Cioè
plottata in fig. 1 (a destra).
No TweetBacks yet. (Be the first to Tweet this post)